Введение
Для линейки приборов NETZSCH HFM 436 (рис. 1) доступна новая опция, позволяющая проводить испытания тепловых расходомеров на образцах, подвергаемых высокой сжимающей нагрузке; эта функция расширяет возможности программ НИОКР по теплоизоляции.
Изменяя давление пластины на образец для достижения различных степеней сжатия, пользователи могут построить кривые теплопроводности в зависимости от плотности, что позволяет получить информацию об относительной силе различных процессов переноса тепла в теплоизоляционных продуктах.
В данном документе представлен анализ трех доминирующих механизмов теплопереноса в волокнистом стеклоизоляционном материале с целью получения аналитического выражения для функциональной зависимости теплопроводности от плотности; прогнозы аналитической модели сравниваются с фактическими данными испытаний HFM, проведенных при различных нагрузках в обновленном HFM 436 Lambda. Отличное согласие наблюдалось во всем диапазоне плотности, который охватывает соотношение 19:1 от самой высокой до самой низкой.

Многорежимная теплопередача в изоляционных материалах
В современном мире, заботящемся о сохранении энергии, постоянно напоминают о важности мер по энергосбережению, одной из которых является улучшение тепловых характеристик зданий с помощью высококачественной изоляции. Усилия производителей в области НИОКР, направленные на разработку теплоизоляции с более высокими характеристиками, значительно выиграли от параллельного развития более мощных экспериментальных и аналитических инструментов для оценки их прогресса. Новые возможности тестирования, о которых идет речь в этой заметке, представляют собой еще один шаг в этом направлении.
В данном исследовании мы анализируем теплопередачу через стекловолоконное одеяло, обычно используемое в качестве теплоизоляции зданий. Такое одеяло представляет собой клубок длинных стеклянных волокон, являющихся матрицей, внутри которой находится воздух.
Проведение через воздух:
При умеренных температурах значительная часть теплопередачи через изоляцию происходит за счет проводимости через воздух, которая не зависит от плотности. Этот режим теплопередачи регулируется уравнением Фурье при постоянной проводимости воздуха λair.
Теплопроводность через стекловолокно:
Теплопередача через стекловолокна также определяется уравнением Фурье, но в этом случае соответствующая теплопроводность glass является функцией плотности ρ. Пути теплопроводности увеличиваются примерно пропорционально плотности, как:
λстекло = B∙ρ
при этом B является константой.
Излучение:
Для режима радиационной теплопередачи стекловолоконное полотно часто рассматривается как поглощающая, излучающая, участвующая и оптически толстая среда с оптическими свойствами, не зависящими от длины волны. При таких допущениях радиационная теплопередача определяется как:
qradiative = -λrad dT/dx
Это уравнение похоже на закон Фурье, поэтому λrad часто называют радиационной теплопроводностью. Чем плотнее одеяло, тем больше количество стекловолокон на единицу объема, что приводит к большему рассеянию и снижению радиационного переноса.
Таким образом, радиационный поток убывает со скоростью, обратно пропорциональной плотности:
λrad = C/ρ
при этом C - постоянная величина.
Общее тепло, передаваемое через одеяло, является суммой этих трех различных режимов. Эффективная теплопроводность определяется как:
λtotal = λair +B∙ρ + C/ρ
Это последнее уравнение представляет собой связь между общей теплопроводностью и плотностью стекловолоконного одеяла с тремя неизвестными параметрами: λair, B и C.
HFM 436 Измерения стекловолоконных одеял с функцией переменной нагрузки
Начиная с изоляционного одеяла из стекловолокна толщиной 240 мм, был вырезан набор квадратных секций размером 300 мм на 300 мм и уложен на разную высоту. Измерения теплопроводности при различной плотности проводились путем изменения толщины с помощью давления на плиту. Для стопок стекловолокна, превышающих максимальное отверстие HFM 436/3 в 100 мм, перед установкой в HFM проводилось предварительное сжатие с помощью жестких пластин. Все измерения проводились при комнатной температуре.libraПрибор был связан со стандартом стеклопластиковой плиты NIST 1450d толщиной 25 мм, а разница температур пластин составляла 20 К.
Результаты и обсуждения
Результаты измерений представлены в таблице 1 и на рисунке 2.
Таблица 1: Зависимость теплопроводности от плотности для образца из стекловолокна, подвергнутого различным сжимающим нагрузкам в аппарате HFM при комнатной температуре
Толщина (мм) | Давление в аппарате HFM | Плотность (кг/м³) | Проводимость (Вт/м*К) | |
|---|---|---|---|---|
(PSI) | (кПа) | |||
| 100.0 | 0.00 | 0.03 | 8.6 | 0.0472 |
| 75.3 | 0.00 | 0.03 | 11.4 | 0.0418 |
| 50.1 | 0.00 | 0.03 | 12.6 | 0.0394 |
| 50.3 | 0.03 | 0.19 | 17.1 | 0.0369 |
| 50.4 | 0.05 | 0.35 | 30.2 | 0.0333 |
| 24.7 | 0.10 | 0.68 | 34.8 | 0.0325 |
| 17.3 | 0.22 | 1.51 | 49.6 | 0.0318 |
| 49.1 | 0.12 | 0.85 | 52.6 | 0.0317 |
| 50.0 | 0.67 | 4.63 | 87.1 | 0.0317 |
| 50.1 | 1.58 | 10.9 | 125 | 0.0325 |
| 38.2 | 3.09 | 21.3 | 164 | 0.0330 |
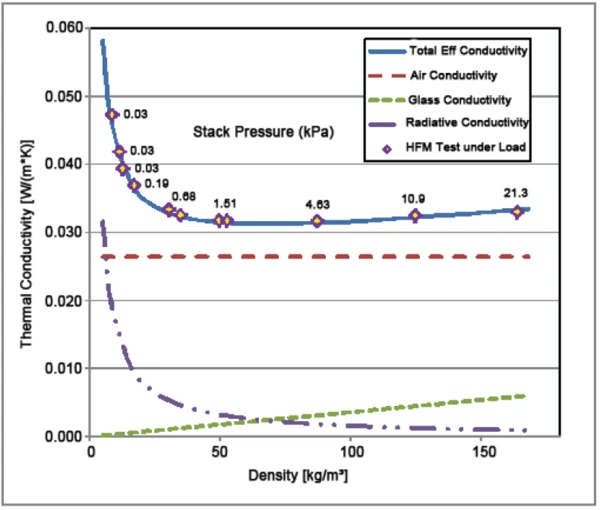
Синяя кривая была получена путем подгонки точек данных к модели общей проводимости с помощью метода наименьших квадратов. Можно сделать вывод, что представленная выше модель является адекватной формулировкой процесса теплоотдачи через стекловолоконное одеяло. Пунктирные кривые представляют каждый ожидаемый режим переноса. Результаты показывают широкий минимум теплопроводности в диапазоне плотностей примерно 50-80 кг/м3, вблизи плотности, при которой проводимость за счет стекловолокна равна радиационной проводимости. Эта информация может быть использована производителями для оптимизации характеристик продукции путем минимизации содержания стекловолокна и, следовательно, стоимости. Например, оптимальная плотность, вероятно, будет находиться на стороне низкой плотности вблизи минимума проводимости.
Заключение
Очень удобно проводить такое исследование с помощью функции переменной нагрузки. Для тщательного статистического анализа, конечно, потребуется большее количество точек данных, что легко достижимо с помощью HFM 436 Lambda. Можно легко запрограммировать одно полное испытание с различными нагрузками и температурами. Это применение также распространяется на другие пористые изоляционные материалы, такие как каменная (минеральная) или шлаковая вата.