Introduction
A new option is available for the NETZSCH HFM 436 line of instruments (figure 1) that enables users to conduct heat flow meter tests on samples subjected to high compressive loads; this feature expands the range of possibilities for R&D programs on thermal insulations.
By varying the plate pressure on the sample to achieve different levels of compression, users can generate curves of thermal conductivity as a function of density, revealing information on the relative strength of different heat transport processes in thermal insulation products.
This Application Note provides an analysis of the three dominant heat transport mechanisms in a fibrous glass insulation material in order to derive an analytical expression for the functional dependence of thermal conductivity on density; predictions of the analytical model are compared against actual HFM test data generated under various loads in the updated HFM 436 Lambda. Excellent agreement was observed over the entire density range, which spanned a ratio of 19:1 from highest to lowest.

Multi-Mode Heat Transfer within Insulation Materials
In today’s energy-conscious world, there are constant reminders of the importance of energy conservation measures – a key one of which being to enhance the thermal performance of buildings with high quality insulation. R&D efforts of manufacturers aimed at developing higher performance thermal insulations have benefited greatly from the parallel development of more powerful experimental and analytical tools for assessing their progress. New testing capabilities discussed in this application note represent another step in that direction.
In this current study, we analyze the heat transfer through a glass fiber blanket, commonly used as building insulation. Such blanket is a tangle of long glass fibers that constitute the matrix within which air is entrapped.
Conduction through air:
At moderate temperatures, a signifi cant portion of heat transfer across the insulation occurs by conduction through air, which is independent of density. This heat transfer mode is governed by the Fourier equation with a constant air conductivity λair.
Conduction through the glass fibers:
The heat transfer through the glass fi bers is also governed by the Fourier equation, but in this case, the corresponding thermal conductivity glass is a function of the density ρ. The conductive pathways increase roughly in proportion to the density as:
λglass = B∙ρ
with B being a constant.
Radiation:
For the radiative heat transfer mode, the glass fiber blanket is often considered as an absorbing, emitting, participating and optically thick media with wavelength independent optical properties. With these assumptions, the radiative heat transfer is derived as:
qradiative = -λrad dT/dx
This equation is similar to the Fourier law, which is the reason why λrad is often referred to as the radiative thermal conductivity. The denser the blanket, the bigger the number of glass fibers per unit volume, resulting in more scattering and a lowering of the radiative transfer.
The radiative flux thereby decays at a rate that is inversely proportional to the density:
λrad = C/ρ
with C being a constant.
The total heat transferred through the blanket is the sum these three distinct modes. The effective thermal conductivity is then derived as:
λtotal = λair +B∙ρ + C/ρ
This last equation represents the relationship between the total conductivity and the density of the glass fiber blanket with three unknown parameters: λair, B and C.
HFM 436 Fiberglass Blanket Measurements with Variable Load Feature
Starting with a 240 mm thickness fiberglass insulation blanket, a set of 300 mm by 300 mm square sections were cut and stacked to various heights. Thermal conductivity measurements with diff erent density were performed by varying the thickness through the plate pressure. For fiberglass stacks which exceeded the 100 mm maximum opening of the HFM 436/3, pre-compression was performed with rigid plates before installation in the HFM. All measurements were conducted at room temperature. The instrument was calibrated with a 25 mm thickness NIST 1450d fiberglass board standard and the plate temperature difference was 20 K.
Results and Discussions
The results of the measurements are presented in table 1 and figure 2.
Table 1: Thermal conductivity versus density for a fiber glass sample subjected to various compressive load settings in an HFM apparatus at room temperaure
Thickness (mm) | HFM Stack Pressure | Density (kg/m³) | Conductivity (W/m*K) | |
|---|---|---|---|---|
(PSI) | (kPa) | |||
| 100.0 | 0.00 | 0.03 | 8.6 | 0.0472 |
| 75.3 | 0.00 | 0.03 | 11.4 | 0.0418 |
| 50.1 | 0.00 | 0.03 | 12.6 | 0.0394 |
| 50.3 | 0.03 | 0.19 | 17.1 | 0.0369 |
| 50.4 | 0.05 | 0.35 | 30.2 | 0.0333 |
| 24.7 | 0.10 | 0.68 | 34.8 | 0.0325 |
| 17.3 | 0.22 | 1.51 | 49.6 | 0.0318 |
| 49.1 | 0.12 | 0.85 | 52.6 | 0.0317 |
| 50.0 | 0.67 | 4.63 | 87.1 | 0.0317 |
| 50.1 | 1.58 | 10.9 | 125 | 0.0325 |
| 38.2 | 3.09 | 21.3 | 164 | 0.0330 |
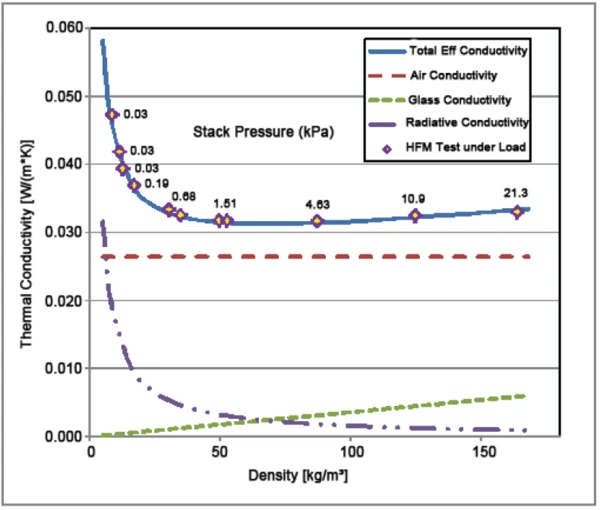
The blue curve was obtained by fitting the data points with the total conductivity model through the least squares method. It can be concluded that the model presented above is an adequate formulation of the heat fl ow process through the glass fiber blanket. The dashed curves represent each expected transfer mode. The results show a broad minimum in thermal conductivity in the density range of approximately 50-80 Kg/m3, near the density where conductivity due to the glass fibers equals the radiative conductivity. This information could be used by manufacturers to optimize their product performance by minimizing the glass fiber content and therefore cost. The optimum density, for example, would probably lie on the low density side of the conductivity minimum.
Conclusion
It is very convenient to conduct such a study with the variable load feature. A rigorous statistical analysis would certainly require more data points, easily achievable with the HFM 436 Lambda. One complete test can be easily programmed with various loads and temperatures. This application also extends to other porous insulation materials like rock (mineral) or slag wool.