DSC para determinar a solubilidade ideal? Diga-me como!

Classificação de medicamentos com base na solubilidade

A solubilidade aquosa é essencial para que um medicamento atinja seu alvo terapêutico, uma vez que a taxa de dissolução influencia diretamente a biodisponibilidade do medicamento. A Farmacopeia dos Estados Unidos e a Farmacopeia Europeia classificam os medicamentos com base em sua faixa de solubilidade aproximada em mg/ml. Por exemplo, 100-1000 mg/ml é a faixa de solubilidade para uma molécula considerada livremente solúvel, e 0,1-1 mg/ml é a faixa para uma molécula de fármaco caracterizada por uma solubilidade em água muito leve. Portanto, a determinação da solubilidade aquosa e não aquosa definirá a melhor abordagem de formulação possível para um bom candidato a medicamento.

A solubilidade ideal fornece a concentração saturada de um soluto, em fração molar, quando um solvente ideal é usado, ou seja, o caso teórico de um soluto sendo dissolvido em um solvente sem nenhuma perda de energia durante o processo de dissolução. Na prática, isso não é possível porque a interação soluto-solvente geralmente não é ideal e a interação química entre o soluto e o solvente pode dificultar o processo de dissolução. Exemplos dessas interações intermoleculares são as ligações de hidrogênio, as propriedades dielétricas e o momento de dipolo.

Embora o método de escolha para determinar a solubilidade de uma molécula seja a espectrofotometria UV, a solubilidade ideal pode ser calculada se o Temperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica).ponto de fusão e a entalpia deTemperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica). fusão da substância forem conhecidos.

No entanto, o que significa solubilidade ideal em termos termodinâmicos?

No processo de dissolução, as ligações soluto-soluto devem ser quebradas. A entrada de energia necessária para quebrar essas ligações é igual à energia necessária para derreter um sólido, ou seja, a entalpia deTemperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica). fusão(_∆Hf). Por outro lado, as ligações solvente-solvente também devem ser quebradas, enquanto as ligações soluto-solvente devem ser formadas. A entrada de energia para essa última etapa pode ser chamada de entalpia de mistura(_∆Hmix). Assim, a entalpia de dissolução é a soma da entalpia deTemperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica). fusão e da entalpia de mistura:

_∆Hsol = _∆Hf + _∆Hmix

Se a entalpia de mistura for igual a zero, então a entalpia de dissolução é igual à entalpia deTemperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica). fusão:

_∆Hsol = _∆Hf

Essas são as principais premissas termodinâmicas para a dissolução ideal de um material cristalino. A dissolução ideal leva à solubilidade ideal.

Outras premissas são que _∆Hf é positivo (aTemperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica). fusão é um evento EndotérmicoUma transição de amostra ou uma reação é endotérmica se for necessário calor para a conversão.endotérmico), assim como _∆Hsol. Entretanto, para que ocorra uma reação espontânea, a energia livre de Gibbs(∆G = _∆Hf -T∆S)deve ser negativa; portanto, a entropia(S) deve ser positiva. Considerando que aTemperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica). temperatura de fusão e a entalpia deTemperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica). fusão são independentes da temperatura experimental, e que a dissolução fornecerá uma solução saturada, a equação de Van't Hoff pode ser aplicada da seguinte forma:

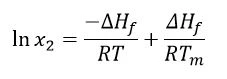
Onde: _x2 = concentração saturada do medicamento em unidades de fração molar

_∆Hf = entalpia deTemperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica). fusão (J/mol)

r = constante do gás (J/K∙mol)

t = temperatura determinada (K)

_tm = temperatura deTemperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica). fusão (K)

O resultado produz a concentração saturada de um soluto no solvente ideal, em fração molar. Em outras palavras, essa seria a concentração máxima alcançável do medicamento no melhor solvente possível. O livro Pharmaceutics de Aulton [1] cita o exemplo do ácido acetilsalicílico. A solubilidade ideal (calculada) do ácido acetilsalicílico é de 0,037 fração molar; o melhor solvente listado é o tetrahidrofurano (THF), cuja solubilidade determinada experimentalmente é de 0,036 fração molar. Portanto, o THF está próximo de ser o solvente ideal para o ácido acetilsalicílico. No entanto, é importante ter em mente que as interações intermoleculares também podem favorecer a dissolução, proporcionando uma solubilidade experimental maior do que a estimada pela equação de Van't Hoff.

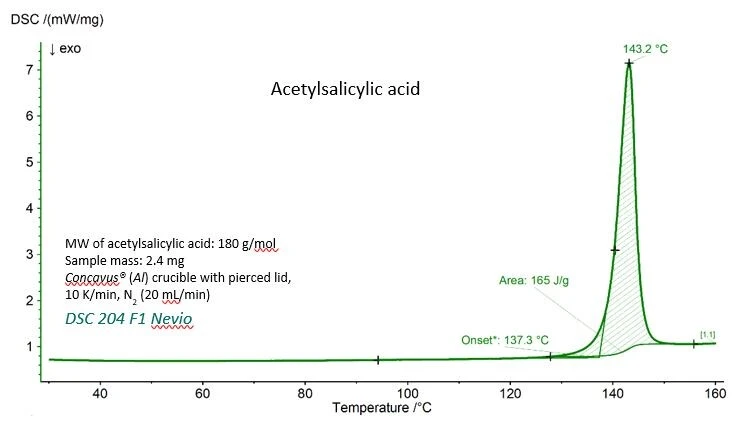
A curva DSC para o ácido acetilsalicílico com os valores experimentais para aTemperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica). temperatura de fusão (temperatura de início extrapolada) e a entalpia deTemperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica). fusão (área sob o pico) é mostrada na figura 1. Ambos os valores concordam muito bem com os valores de referência fornecidos pelo National Institute of Standards and Technology (NIST), como pode ser visto na tabela 1.

Tabela 1 - Valores experimentais e de referência para aTemperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica). temperatura de fusão e a entalpia deTemperaturas e entalpias de fusãoA entalpia de fusão de uma substância, também conhecida como calor latente, é uma medida da entrada de energia, normalmente calor, necessária para converter uma substância do estado sólido para o líquido. O ponto de fusão de uma substância é a temperatura na qual ela muda de estado, passando do sólido (cristalino) para o líquido (fusão isotrópica). fusão do ácido acetilsalicílico.

_{Aspirina (nist.gov)https://webbook.nist.gov/cgi/cbook.cgi?ID=C50782&Units=SI&Mask=4#Thermo-Phase}

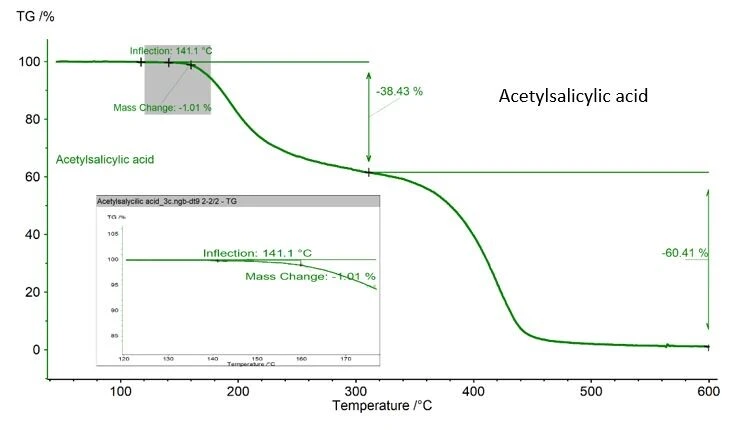
Deve-se tomar cuidado se a substância analisada puder sofrer degradação térmica durante a medição de DSC. No caso do exemplo do ácido acetilsalicílico mostrado aqui, foi registrada uma perda de massa de 1,01%, determinada com um TGA NETZSCH, figura 2. Esse valor é aceitável, pois a ASTM 928 estipula 1% como a massa máxima na faixa de fusão. Se o TGA não estiver disponível, pesar o cadinho e a amostra antes e depois da medição é a melhor maneira de monitorar a perda de massa.

Compartilhe este artigo: