Введение
Механические свойства полимеров часто улучшаются за счет добавления волокон. Получаемое в результате увеличение жесткости, прочности и модуля ползучести позволяет реализовать множество сложных приложений. Если при статических механических испытаниях используются различные режимы нагрузки (растяжение, давление, сдвиг или изгиб), то при динамическом механическом анализе (ДМА) испытания проводятся почти исключительно в режиме изгиба из-за высокой жесткости образца. Однако с помощью высоконагрузочного DMA GABO Eplexor® эти материалы можно часто испытывать и на растяжение. Поэтому в данном приложении более подробно рассматриваются различия между поведением композита при растяжении и изгибе.
В качестве примера был исследован полипропиленовый стекловолокнистый композит с объемной долей волокон 45 %. Как видно на рисунке 1, это слоистая структура [0/90/0/90/0/90/0] с внешними волокнами, лежащими в направлении нагрузки.

Измерение DMA
Образцы имели размеры 55 x 10 x 1,8 мм и характеризовались растяжением и изгибом. Для измерений использовались жесткие держатели образцов на растяжение, позволяющие выдерживать испытательную нагрузку до 150 Н.
Испытания проводились в температурном диапазоне от -100°C до +200°C при скорости нагрева 2 К/мин. Для достижения максимального эффекта измерений образец зажимается при растяжении до свободной длины 35 мм. В обоих испытаниях устанавливается амплитуда динамической деформации 0,1% при частоте 1 Гц. Однако в режиме растяжения амплитуда ограничивается также программируемым пределом силы в 150 Н. В обоих испытаниях программируется статическая сила, которая ведет себя пропорционально динамической силе. Поскольку статическая сила при изгибе должна обеспечивать достаточное сжатие в опорах, коэффициент пропорциональности, PF, при изгибе selectдолжен быть несколько выше (PF растяжения 1,1, PF изгиба 1,2 с FStat=PF*FDyn).
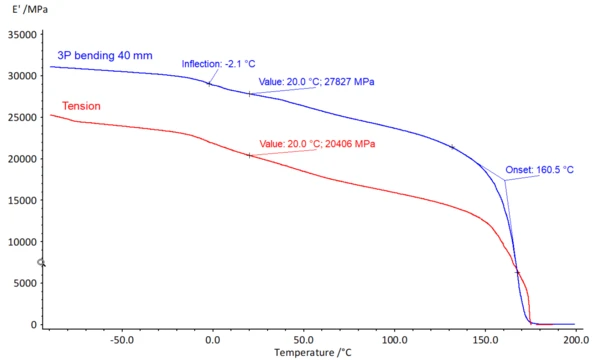
Модуль упругости полимерной матрицы указывает на стеклование при температуре -2°C, что можно определить по точке перегиба (рис. 2). При 160°C (экстраполированное начало отсчета) модуль упругости резко снижается, и материал размягчается.
Очевидно, что модуль упругости при изгибе (синяя кривая) выше, чем при растяжении (красная кривая) практически во всем диапазоне температур. При комнатной температуре (20°C) модуль упругости при изгибе составляет 27827 МПа, что более чем на 30% превышает значение при растяжении (20406 МПа). Такое поведение объясняется асимметричной слоистой структурой образца (сравните рисунок 1). Поскольку внешние волокна при изгибе вносят гораздо больший вклад, чем материал в центре, внешние волокна в направлении нагрузки оказывают на образец эффект жесткости.
Этот эффект часто используется при проектировании для достижения высокой жесткости на изгиб при малом весе. Однако при испытаниях композитных материалов этот эффект означает, что модуль упругости, измеренный при изгибе, строго говоря, действителен только для той толщины образца, которая используется. В режиме растяжения, напротив, отдельные волокна нагружаются равномерно, и можно определить модуль, действительный для всего образца. В связи с этим рекомендуется проводить испытания композитов в зависимости от их последующей нагрузки. DMA GABO Eplexor® предлагает все возможности для этого.
Общая информация о напряженном состоянии образца
Поскольку различие в поведении образца при растяжении и изгибе обусловлено его внутренней структурой, далее будут подробно рассмотрены напряжения, действующие на образец. В данном случае речь идет только о напряжениях в продольном направлении. В частности, для адгезии волокон с полимерной матрицей интерес представляют и другие напряжения.
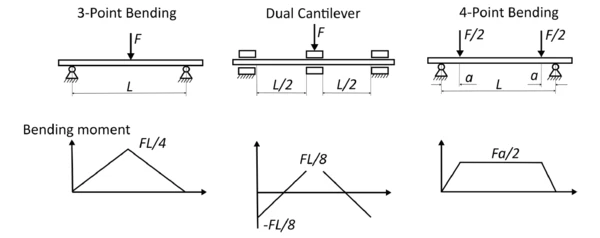
В инженерной механике нагрузка на образец рассчитывается на основе внутренних сил. При растяжении постоянная нормальная сила действует на весь образец. На рисунке 3 показаны внутренние силы для трех изгибаемых подшипников, используемых в DMA. Очевидно, что максимальная нагрузка при 3-точечном изгибе возникает непосредственно под центральной точкой приложения силы; во всем остальном преобладает smaller нагрузка. Поэтому симметричный 4-точечный изгиб также используется для исследования композитов, зависящих от нагрузки [1].
Внутренние напряжения в продольном направлении прямо пропорциональны изгибающему моменту, а также зависят от геометрии и структуры образца. Таким образом, напряжение в образце, которое изменяется по сечению, можно рассчитать в любой точке образца.
На рисунке 4 показаны напряжения, которые будут действовать при модулях, измеренных в приведенном выше примере, при номинальной деформации 0,1 % в однородном материале с линейным упругим поведением материала. При растяжении постоянное напряжение преобладает по всему сечению, а при изгибе образец нагружается на сжатие с верхней стороны и на растяжение с нижней стороны. Соответственно, указанные деформации и напряжения при изгибе также всегда относятся к максимальным значениям во внешнем волокне.
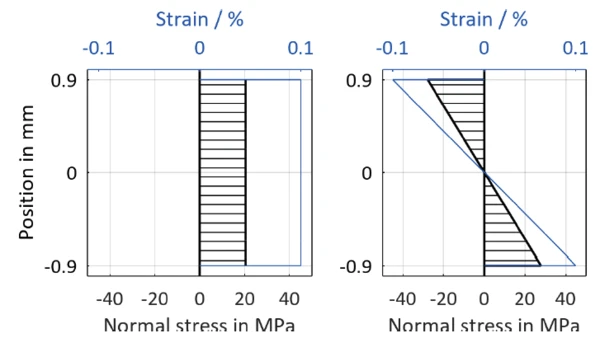
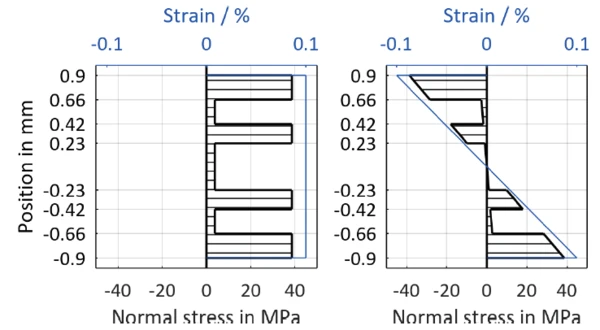
Однако в слоистом композите распределение напряжений гораздо сложнее, чем в однородном образце. Для дальнейших рассуждений в соответствии с теорией балок и слоистых материалов classical предполагается, что поперечные сечения не деформируются, т.е. продольная деформация равномерно распределена по сечению [2].
В приведенном выше измерении модуль запаса при растяжении был измерен иначе, чем при изгибе. Используя формулы инженерной механики (подробнее см. [2]), можно определить, как измеренный модуль при растяжении или изгибе складывается из этих двух компонентов для известной слоистой структуры, состоящей из двух материалов или направлений волокон. Таким образом, два измерения приводят к двум уравнениям, из которых можно определить два модуля материала. Поскольку этот расчет основан на предположении модели, описанном выше, и, кроме того, геометрия и измеренные значения подвержены неопределенности, эта процедура может привести к отклонениям от реальных значений в принципе. При температуре 20°C таким образом можно рассчитать модуль упругости для волокон в направлении нагрузки ЕІІ =38000 МПа и в поперечном направлении ЕІ =3700 МПа.
Эти модули затем можно использовать для расчета напряжений в поперечном сечении образца при заданной деформации. Возникающие при этом скачки в ходе напряжений обусловлены различием модулей отдельных слоев и типичны для волокнистых композитов. Кроме того, из хода напряжений видно, что внешние волокна оказывают особенно сильное влияние на изгибную жесткость образца.
Заключение
При испытании композитов на изгиб преобладает влияние внешних поверхностных слоев. Поэтому результаты измерений при изгибе могут быть обобщены на другие геометрии или случаи нагружения лишь в малой степени. При растяжении, напротив, образец нагружается равномерно, и измеряется только модуль, усредненный по сечению. Соответственно, материалы всегда должны испытываться в соответствии с будущим применением.
С помощью DMA GABO Eplexor® можно измерять изгиб и растяжение относительно жестких композитов. Как и в случае со статическими испытаниями на растяжение, показатели материала могут быть определены при растяжении, если это предпочтительно. Это позволяет получить значительно более точную и полную характеристику материала, чем при использовании приборов smaller, в которых жесткие образцы могут быть измерены только при изгибе.