Introduction
The mechanical properties of polymers are often improved by adding fibers. The resulting increase in stiffness, strength and creep modulus allow for many sophisticated applications to be realized. While in static mechanical testing, different load modes (tension, pressure, shear or bending) are used, in dynamic mechanical analysis (DMA), tests are almost exclusively carried out in bending mode due to the high sample stiffness. With the High-Load DMA GABO Eplexor®, however, these materials can also frequently be tested in tension. In this application note, the differences between the behavior of a composite in tension versus bending mode are therefore discussed in more detail.
As an example, a polypropylene glass-fiber composite with a fiber volume proportion of 45% has been investigated. As can be seen in figure 1, this is a [0/90/0/90/0/90/0] layer structure with the outer fibers lying in the load direction.

DMA Measurement
The samples had dimensions of 55 x 10 x 1.8 mm and are characterized in tension and bending. For the measurements, stiffened tensile sample holders were used, allowing for test loads of up to 150 N.
Testing is carried out in the temperature range from -100°C to +200°C at a heating rate of 2 K/min. To achieve maximum measurement effects, the specimen is clamped in tension to a free length of 35 mm. In both tests, a dynamic strain amplitude of 0.1% is set at a frequency of 1 Hz. In tension mode, however, the amplitude is limited by the also programmable force limit of 150 N. In both tests, a static force is programmed that behaves proportionally to the dynamic force. Since the static force in bending has to ensure sufficient compression in the supports, the proportionality factor, PF, in bending is selected to be somewhat higher (PF tension 1.1, PF bending 1.2 with FStat=PF*FDyn).
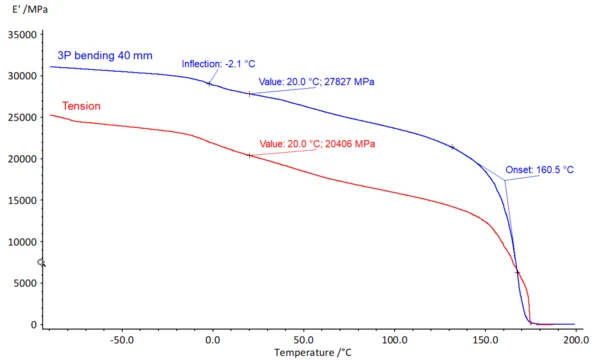
The storage modulus of the polymer matrix material indicates the Température de Transition VitreuseThe glass transition is one of the most important properties of amorphous and semi-crystalline materials, e.g., inorganic glasses, amorphous metals, polymers, pharmaceuticals and food ingredients, etc., and describes the temperature region where the mechanical properties of the materials change from hard and brittle to more soft, deformable or rubbery.glass transition at -2°C, which can be recognized by the inflection point (figure 2). At 160°C (extrapolated onset), the storage modulus sharply decreases, and the material softens.
It is evident that the storage modulus in bending (blue curve) is higher than in tension (red curve) over practically the entire temperature range. At room temperature (20°C), the storage modulus measured in bending occurs at 27827 MPa and is thus more than 30% higher than the value in tension (20406 MPa). This behavior is due to the asymmetric layer structure of the specimen (compare figure 1). Since the outer fibers in bending contribute far more than the material in the center, the outer fibers in the direction of the load have a stiffening effect on the sample.
This effect is frequently used in design to achieve high bending stiffness with low weight. In materials testing for composites, however, this effect means that a modulus measured in bending is, strictly speaking, only valid for exactly the specimen thickness used. In tension mode, on the other hand, the individual fibers are loaded uniformly and a modulus valid for the entire specimen can be determined. Due to this differing effect, it is therefore recommended to test composites according to their subsequent loading. The DMA GABO Eplexor® offers all possibilities for this.
General Information on the Specimen’s State of Stress
Since the differing behavior in tension versus bending is due to the specimen’s internal structure, the stresses acting on the specimen shall be viewed in detail in the following. The presentation is limited to the stresses in the longitudinal direction relevant in this context. For adhesion of the fibers with the polymer matrix in particular, other stresses would also be of interest.
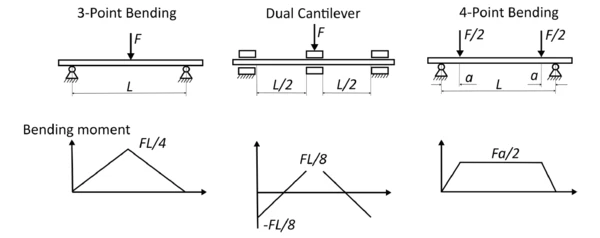
In engineering mechanics, the load of a specimen is calculated on the basis of the internal forces. In tension, a constant normal force prevails over the entire specimen. Depicted in figure 3 are the internal forces for three bending bearings used in the DMA. It is obvious that the maximum load of the 3-point bending used here occurs directly below the central force introduction; everywhere else, a smaller load prevails. Therefore, the symmetrical 4-point bending is also used for investigations of composites dependent upon load [1].
The internal stresses in the longitudinal direction are directly proportional to the bending moment and also depend on the specimen’s geometry and structure. Thus, the ContrainteLa Contrainte est définie par un niveau de force appliquée sur un échantillon d’une section bien définie. (Contrainte = force/surface). Les échantillons qui possèdent une section rectangulaire ou circulaire peuvent être comprimés ou étirés. Les matériaux élastiques comme les élastomères peuvent être étirés jusqu’à 5 à 10 fois leur longueur initiale.stress in the specimen – which varies over the cross-section – can be calculated at any point in the specimen.
Figure 4 shows the stresses that would act with the moduli measured in the above example, at the nominal strain of 0.1% in a homogeneous material with linear elastic material behavior. In tension, a constant stress prevails over the entire cross-section, while in bending, the specimen is loaded in compression on the upper side and in tension on the lower side. Accordingly, the specified strains and stresses in bending also always refer to the maximum values in the outer fiber.
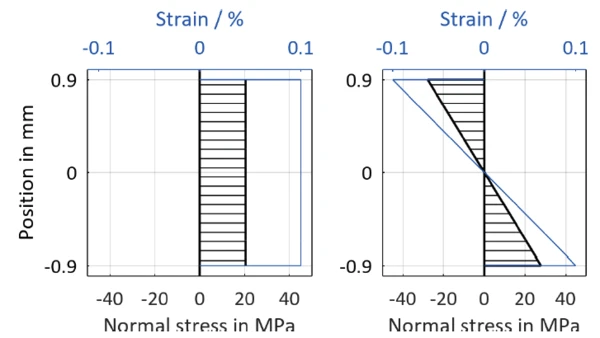
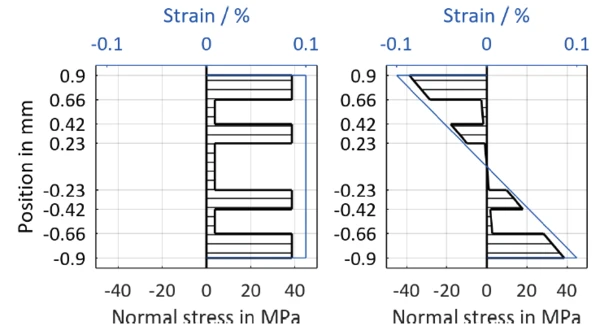
In the layered composite, however, a much more complicated stress distribution occurs than is the case for the homogeneous specimen. For further considerations, it is assumed in accordance with the classical beam and laminate theory that the cross-sectional areas do not warp, i.e., that longitudinal strain is uniformly distributed over the cross-section [2].
In the measurement above, a different storage modulus was measured in tension than in bending. Using the formulas of engineering mechanics (for details, see [2]), it is known how the measured modulus in tension or bending is composed of these two components for a known layer structure consisting of two materials or fiber directions. Thus, the two measurements result in two equations from which the two moduli of the material can be determined. Since this calculation is based on the model assumption explained above and, in addition, geometry and measured values are subject to uncertainties, this procedure may result in deviations from the real values in principle. At a temperature of 20°C, a storage modulus for the fibers in the loading direction of EІІ =38000 MPa and transverse to the loading direction of EІ =3700 MPa can be calculated this way.
These moduli can then be used to calculate the stresses in the cross-section of the specimen at a given strain. The resulting jumps in the course of the stress result from the different moduli of the individual layers and are typical for fiber composites. In addition, it is clear from the course of the stress that the outer fibers have a particularly strong effect on the bending stiffness of the specimen.
Conclusion
When testing composites in bending, the influence of the outer surface layers dominates. Therefore, the results of bending measurements can only be generalized to other geometries or load cases poorly. In tensile mode, on the other hand, the specimen is evenly loaded and only a module averaged over the cross-section is measured. Accordingly, materials should always be tested in accordance with the future application.
By means of the DMA GABO Eplexor®, relatively stiff composites can be measured in bending and tension. As is also the case for static tensile tests, the material values can thus be determined in tension, as preferred. This allows for a significantly more precise and complete characterization of the material than would be the case with smaller instruments, in which stiff specimens can be measured in bending only.