Introduction
Today, the method of Dynamic-Mechanical Thermal Analysis (DMTA) is very well established in laboratories of materials research, development and quality control. The DMTA technique allows for the observation of the frequency and the elongation-dependent mechanical properties (both linear and non-linear) of, for example, filled and unfilled rubber compounds. The instrument of choice here is the successful Eplexor® 500 N by NETZSCH GABO Instruments.
Application
Temperature sweeps in the compression, tension or shearing mode clearly show the temperature dependency of the mechanical properties of rubbers and rubber mixtures. In most cases, the samples are cooled down to an initial temperature below Tg (Température de Transition VitreuseThe glass transition is one of the most important properties of amorphous and semi-crystalline materials, e.g., inorganic glasses, amorphous metals, polymers, pharmaceuticals and food ingredients, etc., and describes the temperature region where the mechanical properties of the materials change from hard and brittle to more soft, deformable or rubbery.glass transition temperature) and are then heated to the final temperature using a low constant heating rate (1 to 3 K/min), in order to achieve homogeneous temperature distributions within the samples.
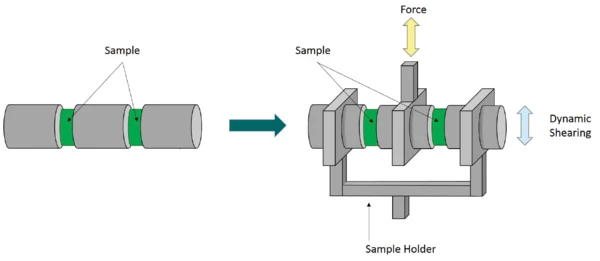
The following investigations were carried out in shear geometry: In the double-shear device (see figure 1), two cylindrical rubber samples (thickness: 2 mm, diameter: 10 mm) are placed and glued between two metallic supports which are firmly connected to the shear-type sample holder. Two different loading modes can be applied:
- Force-controlled dynamic load (this means under constant force)
- Strain-controlled dynamic load (this means under constant strain)
In the first case, the sample is subjected to a fixed dynamic force. At temperatures below the Tg, the sample deformation is small due to the high stiffness of rubbers and rubber mixtures in the glassy state. With increasing temperature, the sample softens and its deformation under constant force increases.
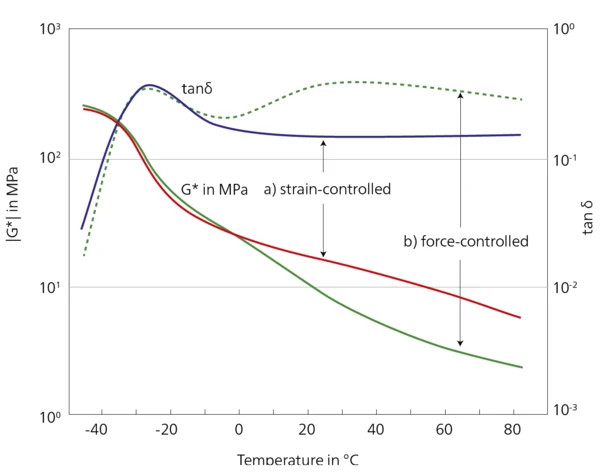
In the second case, the sample is subjected to a constant strain over the entire measuring range. The application of constant strain requires the application of high levels of force at temperatures below the glass transition. As temperature increases, the applied force decreases due to softening of the sample. Figure 2 displays differences between strain- and force-controlled runs. The imposed strain of 0.25% related to sample thickness corresponds to a real deformation of approx. 5 μm. At this relatively small deformation, approx. 25 N have to be applied at low temperatures. This test clearly demonstrates that even for a shear test without preload, a sufficient force reserve must be available. The curve progression in the force-controlled mode deviates significantly from the results of the strain-controlled mode. The two modes generate different physical test conditions and induce a different material response. The high strain caused by the constant-force mode dis-tinctly reflects the dependence of the amplitude on the mechanical properties of the rubber samples. In the force-controlled mode, the resulting strains are higher than in the strain-controlled mode by a factor of 10.
Results
In order to investigate strain-dependent mechanical properties with the necessary accuracy and resolution, analyzers with a sufficient force reserve are required such as the Eplexor® 500 N by NETZSCH GABO Instruments. In addition, suitable control systems that generate and control the strain with high accuracy in the μm-range are of high importance. Whereas the results of force-controlled measurements show an additional structure above the Tg, the strain-controlled measurements are almost free of it. Here, it is necessary to keep in mind that at constant force, the defor-mation can become larger than in the constant strain case. Other deformation mechanisms and thermal effects which complicate interpretation of the material behavior become involved. The constant strain case is more clearly defined, as the deformation is always maintained at the same amplitude during the entire experiment. It is obvious that the strain-controlled measurement mode is beneficial for investigating the properties of rubbers and rubber mixtures. To obtain reliable information about the shear modulus (and tanδ) above the glass transition, the deformation should be constant during temperature sweeps.