Введение
Экструзия, литье под давлением и компрессионное формование - все эти процессы зависят от вязкости материала, т.е. его сопротивления течению. Однако вязкость влияет не только на процесс обработки, но и на механические характеристики конечного продукта. В частности, молекулярная масса и вязкость тесно связаны между собой.
Далее три различных материала PEEK классифицируются в зависимости от их молекулярной массы с помощью измерений колебаний на ротационном реометре Kinexus.
Условия измерения
Частотные измерения проводились для трех материалов, обозначенных как PEEK 1, PEEK 2 и PEEK 3. Деформация (или напряжение), приложенная к образцу, должна быть достаточно низкой, чтобы не разрушить структуру образца, и чтобы измерения проводились в пределах линейно-вязкоупругого диапазона (Линейная вязкоупругая область (LVER)В LVER приложенные напряжения недостаточны для того, чтобы вызвать структурное разрушение (текучесть) конструкции, поэтому измеряются важные микроструктурные свойства.LVER). Амплитудная развертка служит в качестве предварительного измерения для определения предела Линейная вязкоупругая область (LVER)В LVER приложенные напряжения недостаточны для того, чтобы вызвать структурное разрушение (текучесть) конструкции, поэтому измеряются важные микроструктурные свойства.LVER. В таблице 1 приведены условия амплитудной и частотной развертки.
Таблица 1: Условия проведения измерений колебаний
| Амплитудная развертка | Частотная развертка | |
|---|---|---|
| Устройство | Kinexus ultra+ с камерой с электрическим нагревом | |
| Геометрия | PP25 (пластина-пластина, диаметр: 25 мм) | |
| Зазор | 500 мкм | 500 мкм |
| Температура | 360°C | 360°C |
| Деформация сдвига | от 1 до 100% | - |
| Напряжение сдвига | - | 1 000 Па (ПЭЭК 1), 500 Па (ПЭЭК 2 и 3) |
| Частота | 1 Гц | от 10 до 0,01 Гц |
| Атмосфера | Азот (1 л/мин) | |
Амплитудная развертка: Определение LVER (линейный вязко-эластичный диапазон)
На рис. 1 показаны кривые, полученные в результате амплитудной развертки на PEEK 1 в зависимости от деформации сдвига. При деформации сдвига до 30 % - что соответствует напряжению сдвига около 10 000 Па - модуль упругости при сдвиге G´ остается постоянным, что свидетельствует о том, что материал находится в состоянии Линейная вязкоупругая область (LVER)В LVER приложенные напряжения недостаточны для того, чтобы вызвать структурное разрушение (текучесть) конструкции, поэтому измеряются важные микроструктурные свойства.LVER. Уменьшение G´ при более высоких деформациях сдвига связано с разрушением структуры образца. Для следующей развертки частоты напряжение сдвига 1 000 Па selected.
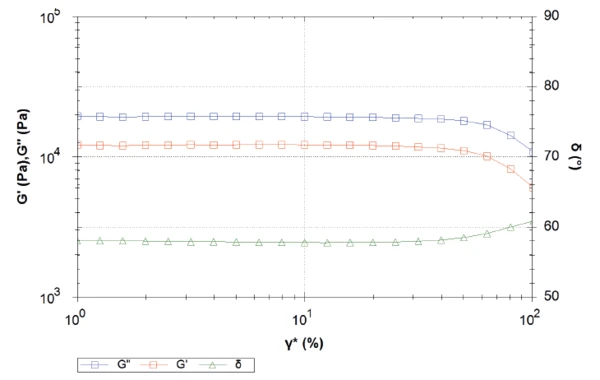
Частотная развертка
На рис. 2 показаны кривые модулей сдвига упругости и потерь, а также фазовый угол при частотной развертке материала PEEK 1. В направлении низких частот модуль сдвига потерь преобладает над модулем сдвига упругости, что приводит к фазовому углу более 45°C. Кривые G' и G" пересекаются на частоте 15 Гц. Здесь материал переходит из жидкого состояния, в котором полимерные цепи успевают распутаться (низкие частоты), в твердое состояние, в котором цепи сцеплены между собой и ведут себя как сеть (высокие частоты).
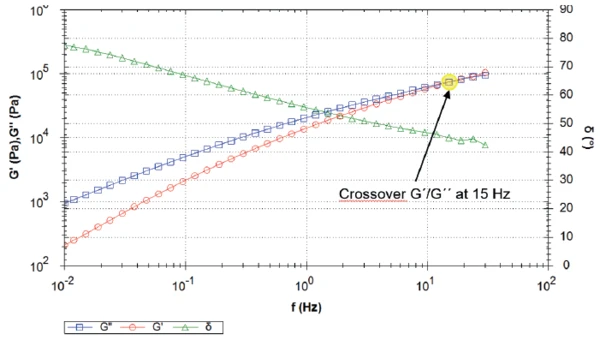
Некоторые определения
G*: Комплексный модуль сдвига
G': Модуль сдвига при хранении, упругий вклад в G*
G": Модуль сдвига потерь, вязкий вклад в G*
δ: Фазовый угол
Фазовый угол δ (δ = G"/G') - это относительная мера вязких и упругих свойств материала. Он варьируется от 0° для полностью упругого материала до 90° для полностью вязкого материала.
На рисунках 3 и 4 показана частотная развертка образцов ПЭЭК 2 и 3 при тех же условиях. Полученные кривые обоих материалов очень похожи и отличаются от первого образца. Во время всего измерения вязкий модуль сдвига (G") преобладает над упругим модулем сдвига (G'), что приводит к фазовому углу (δ), превышающему 45°. В направлении более низких частот фазовый угол увеличивается и достигает почти максимального значения 90°. Другими словами, на низких частотах (или в дальних масштабах) образец ведет себя как почти чисто вязкая жидкость без каких-либо упругих свойств. В измеренном диапазоне частот кроссовер не обнаружен, однако при более высоких частотах он, вероятно, существует, поскольку кривые G´ и G" стремятся друг к другу с ростом частоты. Молекулярная масса полимеров связана с положением кроссовера: Чем ниже частота кроссовера, тем выше молекулярная масса.
В данном случае PEEK 1 имеет более высокую молекулярную массу, чем PEEK 2 и PEEK 3. PEEK 2 и PEEK 3 отличаются по значению модуля упругости при сдвиге. Для ПЭЭК 2 он ниже, чем для ПЭЭК 3 во всем диапазоне измеряемых частот (разница более чем в одно десятилетие на частоте 0,01 Гц). Модуль сдвига потерь у ПЭЭК 2 также ниже, чем у ПЭЭК 3. Это приводит к более высокой жесткости ПЭЭК 3.
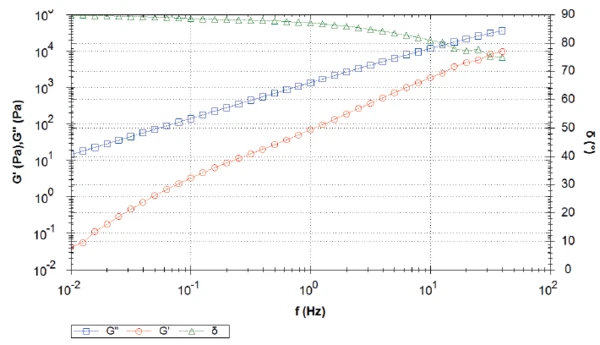
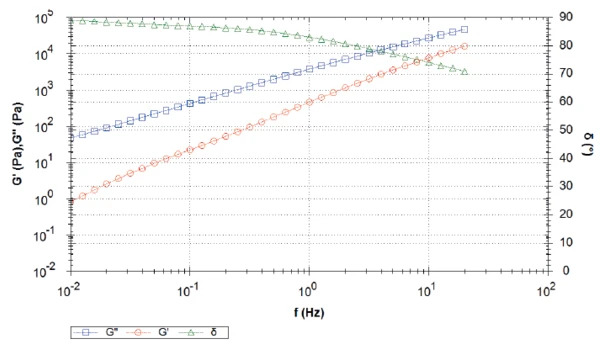
От плато нулевой сдвиговой вязкости до молекулярной массы
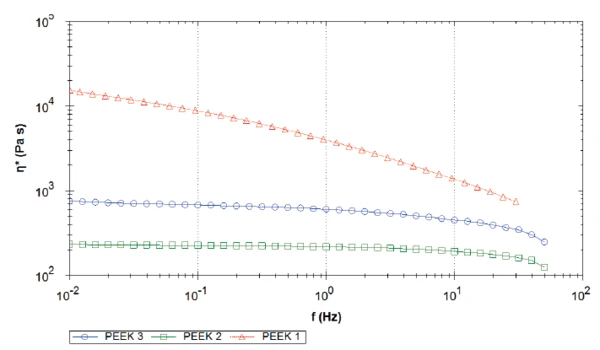
На рисунке 5 сравнивается комплексная вязкость (η) всех трех образцов. Кривые ПЭЭК 1 и ПЭЭК 2 почти параллельны, обе достигают ньютоновского плато в низкочастотном диапазоне и демонстрируют сдвигово-утончающееся поведение на более высоких частотах. Уровень ньютоновского плато связан с молекулярной массой полимера: Чем выше молекулярная масса, тем выше нулевая вязкость. [1]
В отличие от этого, комплексная вязкость (η*) образца 1 продолжает расти с уменьшением частоты, и ньютоновское плато все еще не достигнуто при частоте 0,01 Гц. Более того, для всего измеренного диапазона частот этот материал ПЭЭК демонстрирует более высокую комплексную вязкость с разницей более чем в 1,5 декады по сравнению с образцом 2 при частоте 0,01 Гц.
По уровню плато сдвиговой вязкости всех трех образцов можно сделать вывод, что ПЭЭК 1 имеет более высокую молекулярную массу, за ним следуют ПЭЭК 2 и ПЭЭК 3. Это подтверждает результаты, полученные с помощью кривых G´ и G".
Заключение
Реологическое поведение трех образцов ПЭЭК было охарактеризовано с помощью ротационного реометра Kinexus. Они отличаются по величине плато комплексной вязкости при нулевом сдвиге. Это объясняется различиями в молекулярных массах материалов.