Glossary
Young’s Modulus or Storage Modulus
Young’s modulus, or storage modulus, is a mechanical property that measures the stiffness of a solid material. It defines the relationship between StressStress is defined as a level of force applied on a sample with a well-defined cross section. (Stress = force/area). Samples having a circular or rectangular cross section can be compressed or stretched. Elastic materials like rubber can be stretched up to 5 to 10 times their original length.stress and StrainStrain describes a deformation of a material, which is loaded mechanically by an external force or stress. Rubber compounds show creep properties, if a static load is applied.strain in a material in the linear elasticity region of a uniaxial deformation.
Calculation of Young’s Modulus:
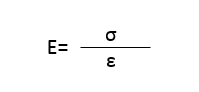
where:
E is Young’s modulus
σ is the uniaxial StressStress is defined as a level of force applied on a sample with a well-defined cross section. (Stress = force/area). Samples having a circular or rectangular cross section can be compressed or stretched. Elastic materials like rubber can be stretched up to 5 to 10 times their original length.stress
ε is the StrainStrain describes a deformation of a material, which is loaded mechanically by an external force or stress. Rubber compounds show creep properties, if a static load is applied.strain along the direction of the applied StressStress is defined as a level of force applied on a sample with a well-defined cross section. (Stress = force/area). Samples having a circular or rectangular cross section can be compressed or stretched. Elastic materials like rubber can be stretched up to 5 to 10 times their original length.stress
Relationship between the Elastic Moduli
E = 2G(1+μ) = 3K(1-2μ)
where:
E is Young’s modulus
G is the shear modulus
K is the bulk modulus
μ is the Poisson number
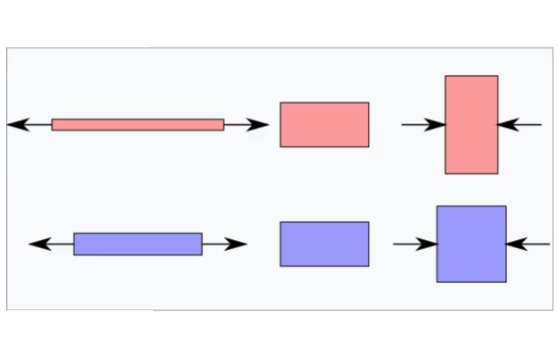
The figure depicts a given uniaxial StressStress is defined as a level of force applied on a sample with a well-defined cross section. (Stress = force/area). Samples having a circular or rectangular cross section can be compressed or stretched. Elastic materials like rubber can be stretched up to 5 to 10 times their original length.stress for tensile (extension, left) or pressure (compression, right). A material with low stiffness (red) provides a higher deformation than a material with high stiffness (blue). Young’s modulus is a measure of the stiffness.