
06.04.2022 by Nishar Hameed, MPhil, PhD CChem, Azadeh Mirabedini, PhD
The Use of Laser Flash Method for Developing Engineered Graphene-based Thermal Interfaces Materials
With a unique set of physical and mechanical properties, graphene, the two-dimensional honeycomb crystal lattice of sp2-hybridized carbon, holds intense academic and industrial interest in developing lightweight, intelligent, and robust hybrid materials. Learn about the use of Laser Flash Method for developing engineered graphene-based thermal interfaces materials and read the scientific paper written by our long-standing customer Swinburne University of Technology, Australia.
Authors: Azadeh Mirabedini, PhD and Nishar Hameed, MPhil, PhD CChem, Smart Materials and Composites Group, Faculty of Science, Engineering and Technology, Swinburne University of Technology, Australia
With a unique set of physical and mechanical properties, graphene, the two-dimensional honeycomb crystal lattice of sp2-hybridized carbon, holds intense academic and industrial interest in developing lightweight, intelligent, and robust hybrid materials. Along with its super strength and featherweight lightness, graphene also benefits from excellent heat and Electrical Conductivity (SBA)Electrical conductivity is a physical property indicating a material's ability to allow the transport of an electric charge.electrical conductivity and is transparent and highly flexible. The intrinsic Thermal ConductivityThermal conductivity (λ with the unit W/(m•K)) describes the transport of energy – in the form of heat – through a body of mass as the result of a temperature gradient (see fig. 1). According to the second law of thermodynamics, heat always flows in the direction of the lower temperature.thermal conductivity of graphene is reported to be in the range of 2000–4000 Wm−1 K−1, mainly depending on its lateral dimensions, crystal quality, and defect concentration, which is among the highest of any known material.[1,2] Fascinatingly, graphene’s Thermal ConductivityThermal conductivity (λ with the unit W/(m•K)) describes the transport of energy – in the form of heat – through a body of mass as the result of a temperature gradient (see fig. 1). According to the second law of thermodynamics, heat always flows in the direction of the lower temperature.thermal conductivity is also found to be alterable with the value increasing logarithmically as a function of the size of graphene conducting pathways within a material. This scarce property has expanded its use in polymer composites and coatings to confer ‘unlimited’ capabilities for a range of thermal management purposes. Given that, graphene-based polymer composites have been reported for use in a range of applications, including thermal interface materials and heat sinks, heat spreaders, thermal greases, coolants, and so on.[3]
Most current graphene production methods are not yet scalable to large quantities, and thus, the use of few-layered graphene (FLG) nanomaterials has recently become one of the most effective, low-cost, and scalable approaches for practical thermal applications.[4,5] FLG retains excellent heat conduction properties while offering a higher cross-section area for the heat flux and can facilitate the formation of the interconnected network of FLG fillers within the polymer matrix, enhancing the thermal performance of the composites.[6]
Heat conduction occurs at the molecular level when heat energy is absorbed by a surface and causes microscopic collisions of particles and transfers the energy to their neighbour particles, a process that will go on as long as heat is being added. Thermal DiffusivityThermal diffusivity (a with the unit mm2/s) is a material-specific property for characterizing unsteady heat conduction. This value describes how quickly a material reacts to a change in temperature.Thermal diffusivity is the most important thermophysical material parameter for characterizing the thermal transport properties of a material. The Laser Flash technique is a non-destructive, contactless, and precise method, which is the most widely accepted for determining the thermal performance of materials at elevated temperatures.
How measurement and modelling come together
Our recent article in the journal of Industrial & Engineering Chemistry Research outlines the application of the NETZSCH LFA 467 HyperFlash®® in the investigation of Thermal DiffusivityThermal diffusivity (a with the unit mm2/s) is a material-specific property for characterizing unsteady heat conduction. This value describes how quickly a material reacts to a change in temperature.thermal diffusivity properties of graphene nanoplatelets (GnP)-modified epoxy polymer nanocomposites. GnPs have an average particle diameter of approx. 25 µm and contain around 18-24 graphene layers. The high data acquisition rate of this device of 2 MHz allows reliable and accurate measurements of high conductive and/or thin materials. Casted nanocomposites were cut into square-shaped specimens with a side length of 10 mm. Their Thermal DiffusivityThermal diffusivity (a with the unit mm2/s) is a material-specific property for characterizing unsteady heat conduction. This value describes how quickly a material reacts to a change in temperature.thermal diffusivity was measured between room temperature and 150°C during the heating and the cooling run. Using the effective medium theory,[7] a simple analytical model was also developed that includes both the Kapitza resistance (also known as interfacial thermal resistance, or thermal boundary resistance), and graphene-graphene Contact ResistanceAccording to the second law of thermodynamics, heat transfer between two systems always moves in the direction from higher to lower temperatures. The amount of thermal energy transferred by heat conduction, e.g., through a wall of a building, is influenced by the thermal resistances of the concrete wall and the insulation layer.contact resistance to calculate the effective Thermal ConductivityThermal conductivity (λ with the unit W/(m•K)) describes the transport of energy – in the form of heat – through a body of mass as the result of a temperature gradient (see fig. 1). According to the second law of thermodynamics, heat always flows in the direction of the lower temperature.thermal conductivity of nanocomposites.
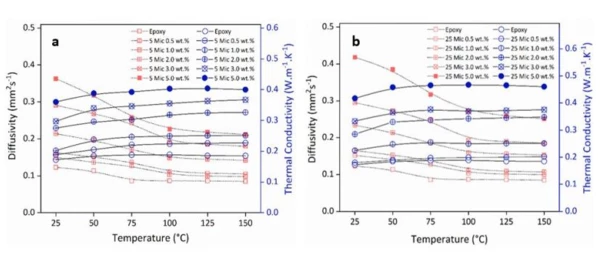
The Thermal ConductivityThermal conductivity (λ with the unit W/(m•K)) describes the transport of energy – in the form of heat – through a body of mass as the result of a temperature gradient (see fig. 1). According to the second law of thermodynamics, heat always flows in the direction of the lower temperature.thermal conductivity of each specimen was then calculated as the product of DensityThe mass density is defined as the ratio between mass and volume. density, Thermal DiffusivityThermal diffusivity (a with the unit mm2/s) is a material-specific property for characterizing unsteady heat conduction. This value describes how quickly a material reacts to a change in temperature.thermal diffusivity, and specific heat of the material. The Thermal ConductivityThermal conductivity (λ with the unit W/(m•K)) describes the transport of energy – in the form of heat – through a body of mass as the result of a temperature gradient (see fig. 1). According to the second law of thermodynamics, heat always flows in the direction of the lower temperature.thermal conductivity of as-prepared GnP-epoxy samples as a function of temperature are shown in Figure 1 (a-b) for nanocomposites containing different loadings of GnP (xGnP M-25 and M-5 abbreviated hereafter GnP25 and GnP5, respectively) (0.5 – 5.0 wt.%).
Why size and loading matters
Thermal conductivity values showed to be enhanced with an increase in GnP loading as well as the particle size, where nanocomposites did not deliver a visible thermal percolation threshold. The new effective Thermal ConductivityThermal conductivity (λ with the unit W/(m•K)) describes the transport of energy – in the form of heat – through a body of mass as the result of a temperature gradient (see fig. 1). According to the second law of thermodynamics, heat always flows in the direction of the lower temperature.thermal conductivity model was then validated with experimental results for randomly-oriented two-phase heterogenous GnP-epoxy nanocomposites. Table 1 comprises the input parameters inserted into the created Thermal ConductivityThermal conductivity (λ with the unit W/(m•K)) describes the transport of energy – in the form of heat – through a body of mass as the result of a temperature gradient (see fig. 1). According to the second law of thermodynamics, heat always flows in the direction of the lower temperature.thermal conductivity models, followed by a correlation of the experimental data with created theoretical thermal models depicted in Figure 2 (a-b) for GnP-epoxy nanocomposites containing GnP25 and GnP5, respectively.

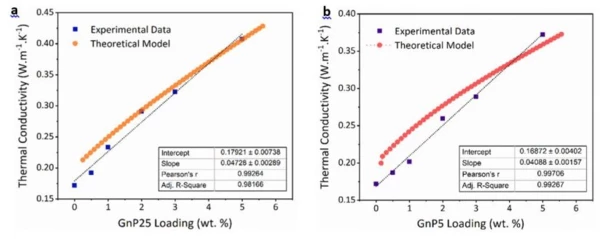
A steady increase in Thermal ConductivityThermal conductivity (λ with the unit W/(m•K)) describes the transport of energy – in the form of heat – through a body of mass as the result of a temperature gradient (see fig. 1). According to the second law of thermodynamics, heat always flows in the direction of the lower temperature.thermal conductivity with an increased filler loading is observed for both the GnP25 and GnP5 particles. In addition, a strong agreement was observed between the predicted values by the Thermal ConductivityThermal conductivity (λ with the unit W/(m•K)) describes the transport of energy – in the form of heat – through a body of mass as the result of a temperature gradient (see fig. 1). According to the second law of thermodynamics, heat always flows in the direction of the lower temperature.thermal conductivity model and experimental data for both types of composites (see Figure 2 (a-b)), with calculated correlation coefficients of ~0.98 and ~0.99 for nanocomposites containing GnP5 and GnP25, respectively. This result proves that the constructed thermal conductivity model in the study can provide a good prediction of the thermal conductivity of GnP-epoxy nanocomposites at different GnP loadings. Increasing the efficiency of manufacturing scalability and extending current material models would assist with designing graphene composite structures with predictable properties and safe failure modes, which in turn facilitate the manufacture of scalable laminate-structured composites for a range of high-end applications such as the aerospace and automotive industries.
This research contributed to a DMTC-managed collaboration involving a network of research and industry partners across Australia. More details can be found in the article: Link to https://pubs.acs.org/doi/abs/10.1021/acs.iecr.1c04621
References
[1] E. Pop, V. Varshney, A. K. a. K. Roy, MRS Bull.2012, 37, 1273.
[2] M. C. Mbambo, S. Khamlich, T. Khamliche, M. K. Moodley, K. Kaviyarasu, I. G. Madiba, M. J. Madito, M. Khenfouch, J. Kennedy, M. Henini, E. Manikandan, M. Maaza, Sci. Rep.2020, 10, 1.
[3] J. Chen, B. Liu, X. Gao, Results Phys.2020, 16, 102974.
[4] A. Mirabedini, A. Ang, M. Nikzad, B. Fox, K. T. Lau, N. Hameed, Adv. Sci.2020, 1903501, 33.
[5] M. Reghat, A. Mirabedini, A. M. Tan, Y. Weizman, P. Middendorf, R. Bjekovic, L. Hyde, D. Antiohos, N. Hameed, F. K. Fuss, B. Fox, Compos. Sci. Technol.2021, 211, 108842.
[6] Z. Barani, F. Kargar, A. Mohammadzadeh, S. Naghibi, C. Lo, B. Rivera, A. A. Balandin, Adv. Electron. Mater.2020, 6, 1.
[7] L. Anderson, P. Govindaraj, A. Ang, A. Mirabedini, N. Hameed, Carbon Trends2021, 4, 100047.
[8] Y. Su, J. J. Li, G. J. Weng, Carbon N. Y.2018, 137, 222.
[9] M. Gresil, Z. Wang, Q. A. Poutrel, C. Soutis, Sci. Rep.2017, 7, 1.