Введение
Двойная дисперсионная лопатка (рис. 1) подходит для образцов, которые необходимо непрерывно диспергировать во время измерения, например, если происходит выраженная седиментация в течение короткого времени. Поскольку скорость сдвига не является полностью равномерной, этот тип геометрии следует рассматривать как более "относительную" геометрию, дающую хорошее представление о вязкости. Напротив, измерения с абсолютной геометрией, как в системе конических пластин, приведут к абсолютным значениям сдвиговой вязкости. Здесь, при абсолютной геометрии, скорость сдвига и напряжение сдвига, приложенное к образцу, четко определяются с помощью измерительного зазора со смещением и крутящим моментом, соответственно. Измерения, проведенные на двух образцах с одинаковой относительной геометрией, можно сравнивать между собой. Однако следует иметь в виду, что они не дают непосредственно абсолютных результатов из-за неоднородности приложенного поля сдвига. В последующем обсуждении будут проведены измерения, демонстрирующие эти различия. Для этого тест, проведенный с абсолютной геометрией, сравнивается с тестом, проведенным с помощью двойного дисперсионного лепестка.

Условия измерения
Измерение вращательного движения (вязкости) проводилось на краске для стен с помощью сдвоенной дисперсионной лопатки (относительная геометрия) и с помощью системы конических тарелок (абсолютная геометрия). В таблице 1 представлены условия, использованные для проведения испытаний.
Таблица 1: Условия измерения
| Образец | Краска для стен | |
| Прибор | Kinexus ultra+ | |
| Геометрия | Абсолют: CP4/40 (Конусная тарелка, диаметр: 40 мм, угол конуса: 4°) | Относительная: Чашка 25 мм, двойная дисперсионная лопатка |
| Зазор | 146 мкм | 5 мм |
| Скорость сдвига | 0.от 1 до 100 с-1 | |
| Температура | 25°C | |
Для всех реометров геометрические константы используются в качестве коэффициентов преобразования, чтобы взять такие параметры прибора, как крутящий момент и перемещение, и преобразовать их в напряжение и скорость сдвига. Для конуса и пластины эти константы хорошо определены1. Для новой геометрии, такой как двухдисперсная лопатка, используемая в данном исследовании, применяется более современная процедура2, позволяющая получить близкое соответствие абсолютной геометрии.
1 Macosko CW: Rheology Concepts, Principles and Applications, Wiley-VCH (1992)
2 Duffy JJ, Hill AJ, Murphy SH: Simple method for determining stress and strain constants for non-standard measuring systems on a rotational rheometer, Appl. Rheol. 25 (2015) 42670.
Результаты измерений
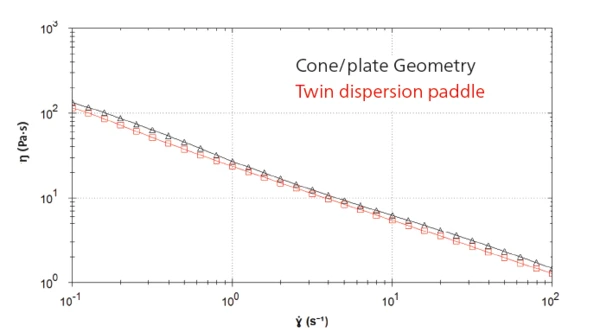
На рис. 2 показаны кривые, полученные в результате обоих измерений при вискозиметрии в установившемся режиме в интервале от 0,1 до 100 с-1. Значения сдвиговой вязкости, полученные с помощью двойного дисперсионного лепестка, отличаются на 10-15 % от абсолютных значений, полученных при измерении с помощью системы конических пластин. Эта погрешность практически постоянна на протяжении всего измерения и ожидается из-за неоднородного профиля сдвига с неабсолютной геометрией. Можно вручную отрегулировать геометрическую константу, чтобы минимизировать это смещение; однако в данном приложении используются значения по умолчанию из обсуждаемого метода2 ,чтобы продемонстрировать ожидаемые различия при использовании новой и относительной геометрии.
Заключение
Для получения значений сдвиговой вязкости лучше всего использовать абсолютную геометрию, например систему конических пластин. Однако если образец очень нестабилен, т.е. происходит седиментация или сепарация, использование абсолютной геометрии может быть ограничено, в то время как двойная дисперсионная лопатка дает более последовательную и репрезентативную информацию о вязкостном поведении образца во время реологических испытаний. В данной работе было показано, что измерения с помощью двойного дисперсионного лепестка приводят к хорошей аппроксимации значений сдвиговой вязкости вещества.