Введение
Напряжение σ, возникающее в результате постоянной деформации ε0, приложенной к полимеру, зависит от времени. [1] Это связано с тем, что полимерные цепи перестраиваются для релаксации напряжений, вызванных деформацией. [2] Как следствие, модуль релаксации зависит от времени:
Более того, если предположить, что повышение температуры не изменяет молекулярные движения, а только ускоряет их [3], то модуль релаксации зависит не только от времени, но и от температуры:
Время и температура тесно связаны. Повышение температуры приводит к увеличению свободного объема между макромолекулами. Таким образом, они будут лучше скользить друг по другу, уменьшая время релаксации материала и другие свойства, например, его вязкость, сопротивление разрушению, модуль сдвига и т. д.
Измерение колебаний
Верхняя пластина колеблется с определенной частотой f [Гц] (или ω [рад/с]) и амплитудой [%] (или деформацией сдвига γ [%]). Определяется напряжение сдвига σ [Па], необходимое для этого колебания. Результат: Определяются вязкоупругие свойства образца, в частности модули упругости и сдвига потерь.
На самом деле, поведение большинства вязкоупругих материалов при одной температуре можно предсказать по изменению временной шкалы [4]. Две различные модели описывают коэффициент сдвига aT, т.е. отношение времен релаксации при температурах T и Tr [2]:
- Сдвиг Аррениуса, справедливый для полукристаллических полимеров и аморфных термопластов при температурах выше Tg + 100 K:
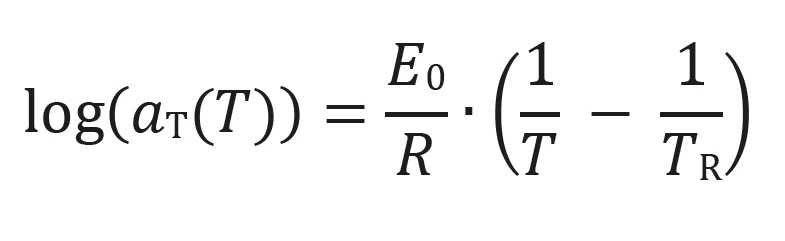
E0: энергия активации релаксации [Дж/моль]; R: газовая постоянная;TR: эталонная температура [K]
- Сдвиг WLF, действительный для температур вблизи стеклования:
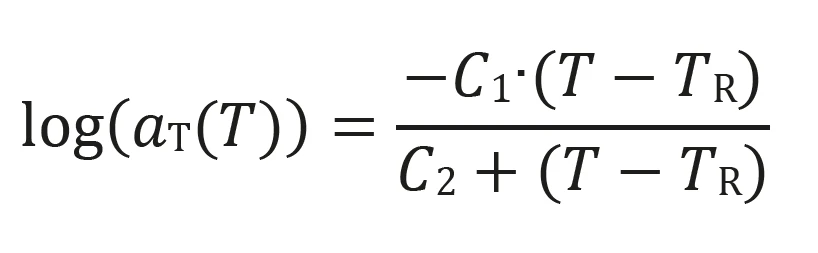
C1, C2: Параметры, зависящие от материала;TR: Контрольная температура [K]
Такая возможность сдвига кривых вязкоупругих свойств очень удобна, поскольку значительно сокращает время измерения. Далее принцип временно-температурной суперпозиции используется для построения эталонной кривой асфальтового вяжущего. Для этого проводятся измерения частотной развертки при различных температурах.
Таблица 1: Условия проведения измерений колебаний
| устройство | Kinexus DSR |
| Режим измерения | Колебания, развертка частоты |
| Геометрия | Пластина-пластина, диаметр: 4 мм (PP4) |
| Зазор | 1.7 мм |
| Температура | -30°C, -15°C, 0°C, 15°C и 30°C |
| Деформация | 0.017%, 0.079%, 0.020%, 0.398%, 0.796% |
| Частота | от 100 до 0,1 рад.с-1 |
Условия и результаты измерений
В таблице 1 приведены условия измерений. На рисунках 1-5 представлены результирующие кривые измерений частотной развертки при пяти различных температурах. На рисунках 6, 7 и 8 сравниваются модуль упругого сдвига, модуль вязкого сдвига и фазовый угол всех измерений.
Чем выше температура, тем ниже модуль упругого сдвига. Как и ожидалось, асфальтовое вяжущее становится жестче с понижением температуры. При 30°C модуль сдвига потерь выше модуля упругого сдвига. При этой температуре "жидкоподобные" свойства материала преобладают над его "твердоподобными" свойствами. Здесь фазовый угол немного превышает 45° во всем диапазоне частот (рис. 1). Материал представляет собой вязкоупругую жидкость.
Измерения при температуре 15°C показывают пересечение упругого и вязкого модуля сдвига на частоте 2,5 рад.с-1 (рис. 2). В этой точке фаза составляет ровно 45°. При более низких частотах, чем частота кроссовера, доминируют жидкоподобные свойства.
Испытания при 0°C, -15°C и -30°C показывают уменьшение фазового угла с понижением температуры. Однако увеличение фазового угла в направлении более низких частот показывает, что для всех температур образец, скорее всего, является вязкоупругой жидкостью. Чем ниже температура, тем позже фазовый угол достигает значения 45°.
Поведение асфальта при 0°C или даже более низких температурах важно для прогнозирования его устойчивости в холодных странах. Для этого решающее значение имеет частота перехода. Однако по практическим соображениям ее невозможно определить экспериментально, поскольку измерение займет слишком много времени. К счастью, применение объясненной временно-температурной суперпозиции позволяет построить мастер-кривую, то есть рассчитать нужные кривые при одной конкретной температуре для более широкого диапазона частот.
На рис. 9 показано построение мастер-кривой модуля упругого сдвига при температуре 0°C. Кривые, измеренные при более низкой (-30°C, -15°C) и более высокой (15°C, 30°C) температуре, чем эта контрольная температура, сдвинуты вправо и влево на коэффициент сдвига aT, соответственно. Другими словами, при повышении температуры процесс релаксации происходит быстрее (смещается в сторону более высоких частот). Расчет основной кривой и коэффициентов, используемых для моделей Аррениуса и WLF, происходит автоматически в программе rSpace (см. табл. 2).
Следует обратить внимание на частоту начала ведущей кривой: 1.6-10-5 рад/с, что означает время более 170 часов (более семи дней!) только для измерения этой единственной точки! Такое испытание было бы нецелесообразно проводить.
Фазовый угол
Фазовый угол δ (tan δ= G"/G´) - это относительная мера вязких и упругих свойств материала. Он варьируется от 0° для полностью упругого материала до 90° для полностью вязкого материала.
Таблица 2: Коэффициенты Аррениуса и WLF, рассчитанные по результатам измерений для базовой температуры 0°C. Коэффициенты WLF k1 и k2 соответствуют C1 и C2 уравнения WLF; коэффициент Аррениуса k1 - коэффициенту E0/R модели Аррениуса.

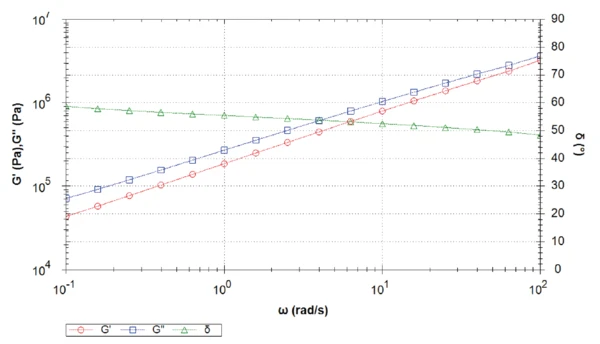
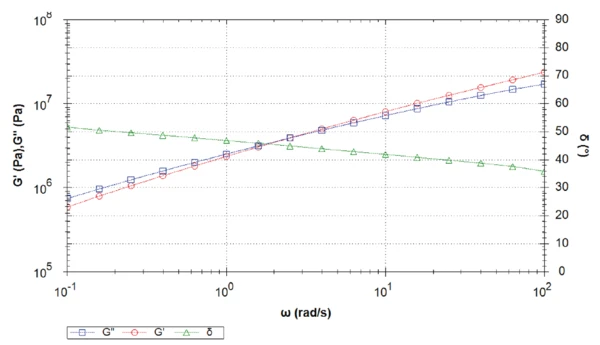
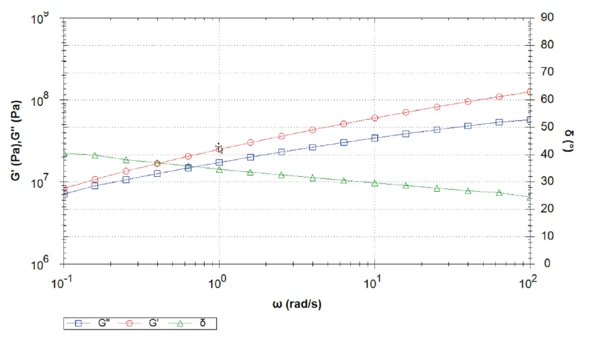
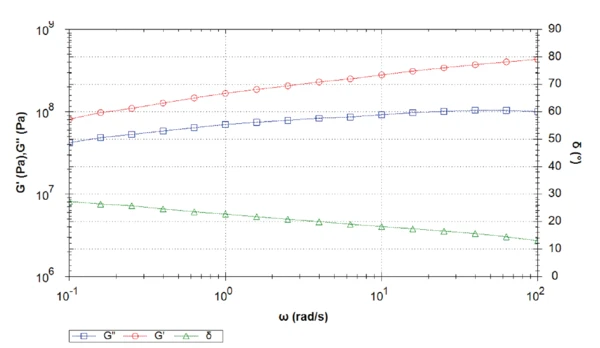
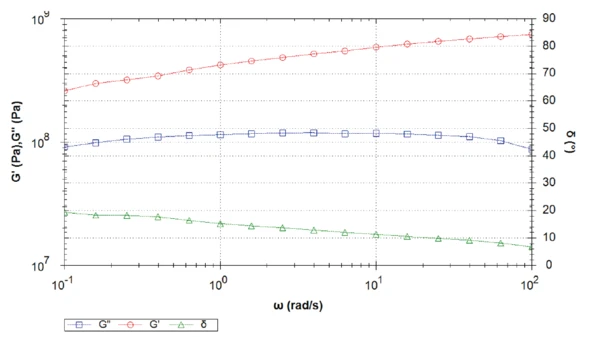
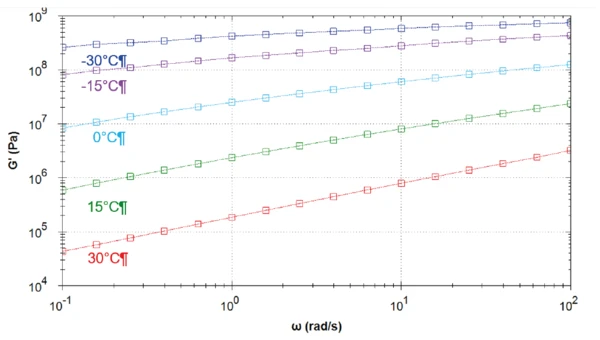
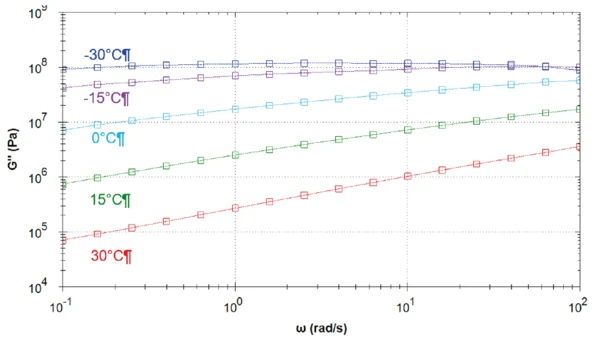
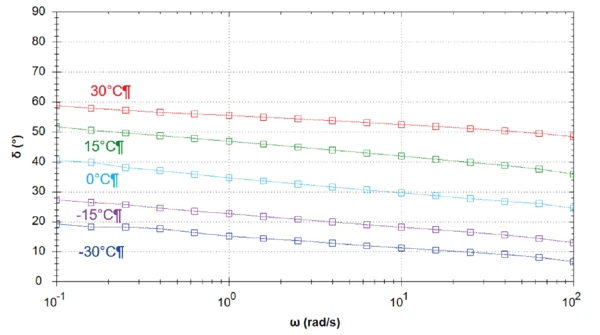
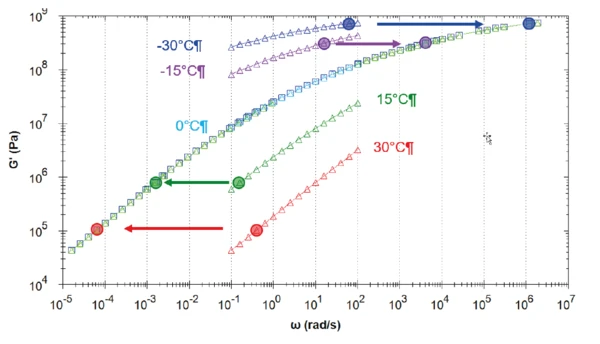
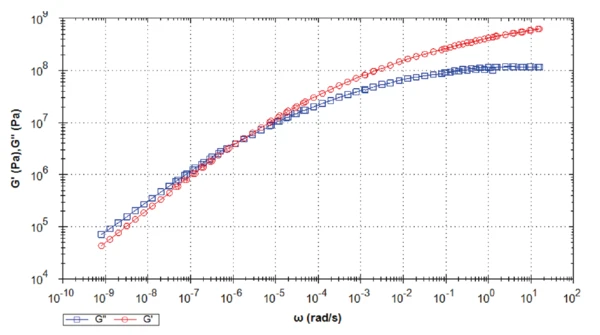
Таблица 3: Перекрестное определение мастер-кривых модулей упругого и вязкого сдвига при различных температурах

На рисунке 10 показана кривая эталонного асфальтового вяжущего для температуры -30°C. Чем ниже температура, тем ниже диапазон частот, достигаемых при расчете. Здесь первая точка находится ниже 10-9 рад-с-1! Переход, обнаруженный между 10-7 и 10-6 рад-с-1, был бы обнаружен только при проведении очень трудоемкого измерения.
В табл. 3 приведены результаты обнаружения кроссовера между упругим и вязким модулями сдвига для всех температур. При указанных температурах асфальт всегда ведет себя как вязкоупругая жидкость. Чем ниже температура, тем ниже частота пересечения, и тем дольше процесс дестабилизации структуры материала.
Если пересечение кривых G' и G'' происходит на частоте 2,4∙10-3 Гц при температуре 0°C, то это соответствует временному масштабу около 7 мин. Это означает, что материал ведет себя преимущественно упруго, если временная шкала короче 7 мин. На практике это означает, что дорога стабильна под нагрузкой в пределах линейного вязко-упругого диапазона. При более длительном времени увеличивается тенденция к деформации материала (образование колеи).
Если данное асфальтовое вяжущее используется в более холодном климате, например, при температуре -30 °C, то пересечение G' и G'' происходит с меньшей частотой, например, увеличивается временная шкала (здесь около 2 месяцев).
Заключение
Вязкоупругое поведение асфальтового вяжущего определялось при температурах от -30°C до 30°C. Чем ниже температура испытания, тем ниже частота кроссовера. Сбор точек данных в низкочастотном диапазоне для получения кроссовера связан с очень большим временем измерения (несколько недель) и поэтому не удобен на практике. Принцип временно-температурной суперпозиции позволил преодолеть эту проблему. Вместо того чтобы проводить бесконечные испытания, измерения колебаний проводились при пяти различных температурах в обычном диапазоне частот. Полученные графики использовались для построения эталонных кривых.