Einleitung
Die Schubspannung σ, die sich aus einer auf ein Polymer aufgebrachten konstanten Deformation ε0 ergibt, hängt von der Zeit ab [1]. Dies liegt daran, dass sich die Polymerketten neu ordnen, um die durch die Verformung verursachten Spannungen abzubauen [2]. Infolgedessen ist der Relaxationsmodul zeitabhängig:
Geht man weiter davon aus, dass ein Temperaturanstieg die Molekularbewegungen nicht verändert, sondern nur beschleunigt [3], ist der Relaxationsmodul nicht nur von der Zeit, sondern auch von der Temperatur abhängig:
Zeit und Temperatur sind eng miteinander verbunden. Ein Temperaturanstieg erhöht das freie Volumen zwischen den Makromolekülen. Dadurch können diese besser übereinander gleiten, wodurch sich die Relaxationszeit des Materials und weitere Eigenschaften, wie beispielsweise Viskosität, Bruchfestigkeit, Schubmodul usw. verringern.
Oszillationsmessung
Die obere Platte oszilliert mit einer definierten Frequenz f [Hz] (oder ω [rad/s]) und Amplitude [%] (oder Scherdeformation γ [%]). Die für diese Oszillation benötigte Schubspannung σ [Pa] wird bestimmt. Ergebnis: Die viskoelastischen Eigenschaften der Probe werden bestimmt, insbesondere Elastizität und Verlustschubmodul.
Tatsächlich lässt sich das Verhalten der meisten viskoelastischen Materialien bei einer Temperatur durch Änderung der Zeitskala von dem bei einer anderen Temperatur vorhersagen [4]. Zwei unterschiedliche Modelle beschreiben den Verschiebungsfaktor aT, d.h. das Verhältnis der Relaxationszeiten bei den Temperaturen T und TR [2]:
- Die Arrhenius-Verschiebung, gültig für semikristalline Polymere und amorphe Thermoplasten bei Temperaturen oberhalb von Tg + 100 K, lautet:
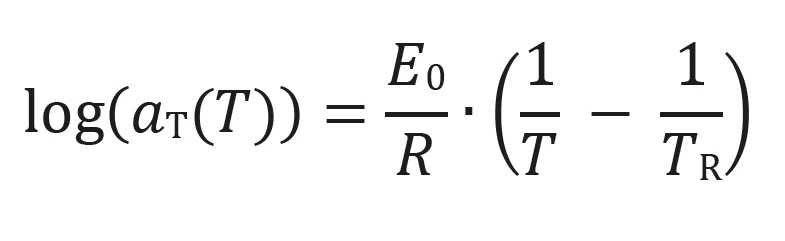
E0: Aktivierungsenergie der RelaxationWhen a constant strain is applied to a rubber compound, the force necessary to maintain that strain is not constant but decreases with time; this behavior is known as stress relaxation. The process responsible for stress relaxation can be physical or chemical, and under normal conditions, both will occur at the same time. Relaxation [J/mol]; R: Gaskonstante; TR: Referenztemperatur [K]
- Die WLF-Verschiebung, gültig für die Temperaturen um den Glasübergang, lautet:
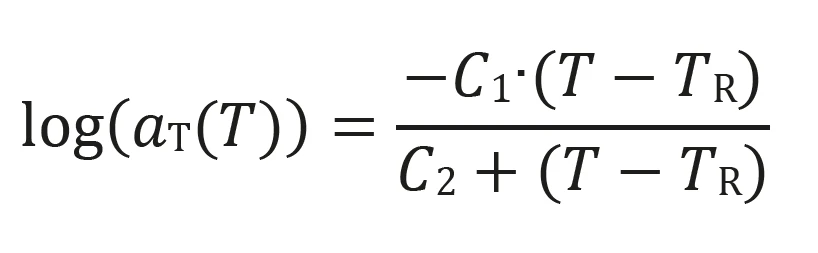
C1, C2: vom Material abhängige Parameter; TR: Referenztemperatur [K]
Die Verschiebung der Kurven einer viskoelastischen Eigenschaft erweist sich als sehr praktisch, da dadurch die Messzeiten erheblich verkürzen werden.
Im Folgenden wird das Prinzip der Zeit-Temperatur- Superposition für die Erstellung einer Masterkurve an einem Asphalt-Bindemittel angewandt. Dazu werden Frequenzsweep-Messungen bei unterschiedlichen Temperaturen durchgeführt.
Tab. 1 Bedingungen der Oszillationsmessungen
| Gerät | Kinexus DSR |
| Messmodus | Oszillation, Frequenzsweep |
| Geometrie | Platte-Platte, Durchmesser: 4 mm (PP4) |
| Messspalt | 1,7 mm |
| Temperatur | -30 °C, -15 °C, 0 °C, 15 °C und 30 °C |
| DehnungDehnung beschreibt die Deformation eines Materials, das durch eine von außen einwirkende Kraft oder Spannung mechanisch belastet wird. Gummimischungen zeigen Kriech-Eigenschaften, wenn eine statische Last aufgebracht wird.Dehnung | 0,017 %, 0,079 %, 0,020 %, 0,398 %, 0,796 % |
| F | 100 bis 0,1 rad.s-1 |
Messbedingungen und -ergebnisse
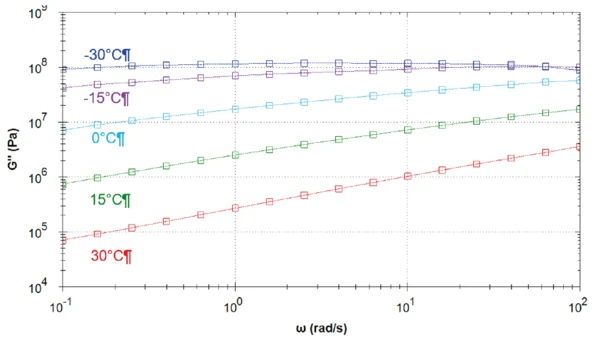
In Tabelle 1 sind die Messbedingungen aufgeführt. Abbildungen 1 bis 5 zeigen die Kurven der Frequenzsweep-Messungen bei fünf verschiedenen Temperaturen. Die Abbildungen 6 bis 8 vergleichen die bei den unterschiedlichen Temperaturen aufgezeichneten elastischen und viskosen Schubmodule sowie die Phasenwinkel.
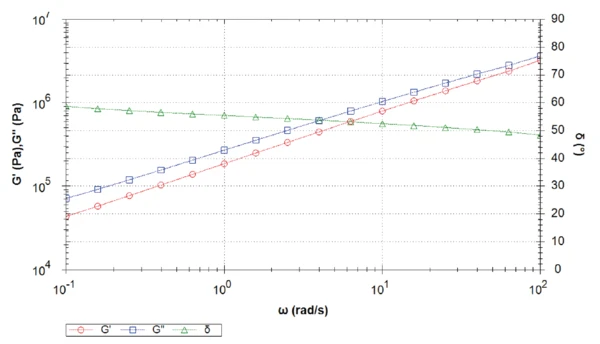
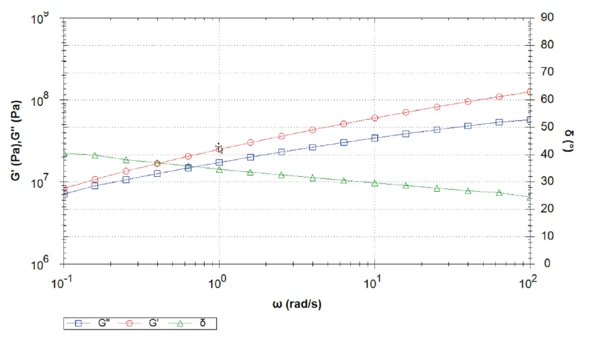
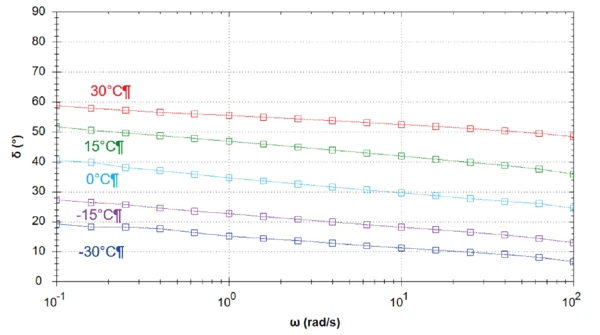
Je höher die Temperatur, desto niedriger ist der elastische Schubmodul. Erwartungsgemäß wird das Asphalt-Bindemittel mit sinkender Temperatur steifer. Bei 30 °C ist der Verlustschubmodul höher als der elastische Schubmodul. Bei dieser Temperatur dominieren die "flüssigkeitsähnlichen" Eigenschaften des Materials die "feststoffähnlichen" Eigenschaten. Hier ist der Phasen- winkel über den gesamten Frequenzbereich etwas größer als 45° (Abb.1). Bei dieser Temperatur ist das Material eine viskoelastische Flüssigkeit.
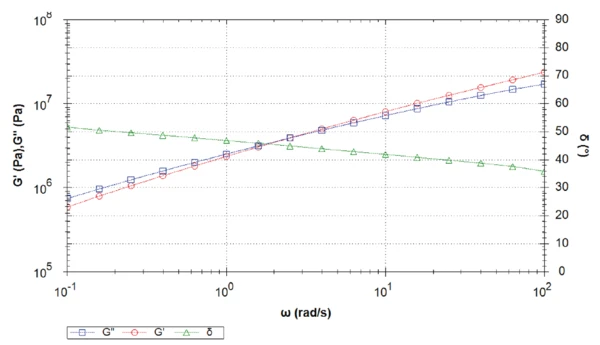
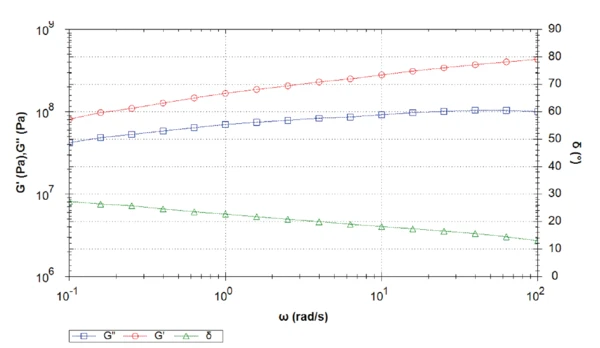
Die Messung bei 15 °C zeigt einen Übergang zwischen elastischem und viskosem Schubmodul bei einer Frequenz von 2,5 rad.s-1 (Abbildung 2). An diesem Punkt beträgt die Phase genau 45°. Bei niedrigeren Frequenzen als dem Frequenzübergang überwiegen die flüssigkeitsähnlichen Eigenschaften.
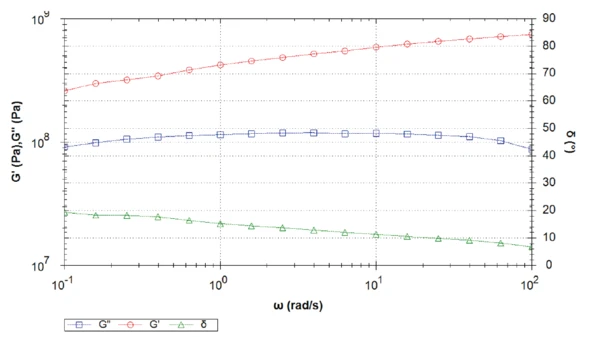
Die Untersuchungen bei 0 °C, -15 °C und -30 °C deuten auf eine Verringerung des Phasenwinkels bei abnehmenden Temperaturen hin. Der Anstieg des Phasenwinkels in Richtung niedrigerer Frequenzen zeigt jedoch, dass sich die Probe bei allen Temperaturen höchstwahrscheinlich wie eine viskoelastische Flüssigkeit verhält. Je niedriger die Temperatur, desto später erreicht er den Wert von 45°.
Die Vorhersage des Materialverhaltens bei 0 °C oder noch niedrigeren Temperaturen ist wichtig, um Aussagen zur Stabilität in kalten Ländern treffen zu können. Daher ist die Frequenzabhängigkeit des Schnittpunkts von ausschlaggebender Bedeutung. Aus praktischen Gründen lässt sich diese jedoch nicht experimentell ermitteln, da die Messungen zu viel Zeit in Anspruch nehmen würden. Glücklicherweise ermöglicht die Anwendung der Zeit-Temperatur-Superposition die Erstellung einer Masterkurve, d.h. die Berechnung der gewünschten Kurven bei einer bestimmten Temperatur für einen breiteren Frequenzbereich.
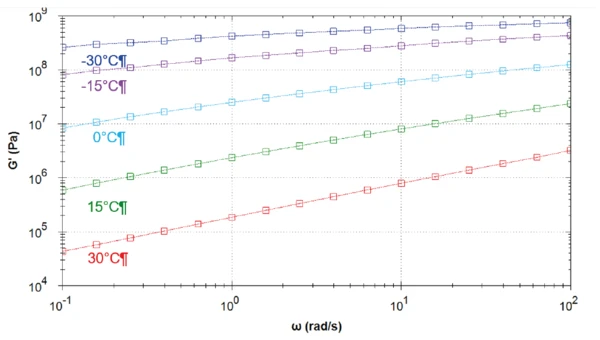
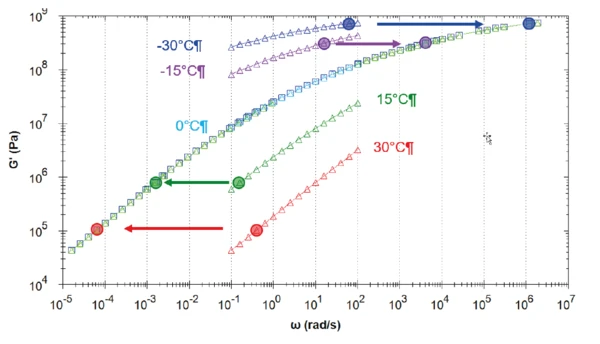
Abbildung 9 zeigt die Erstellung der Masterkurve des elastischen Schubmoduls bei einer Temperatur von 0 °C. Die Kurven, die bei niedrigeren (-30 °C, -15 °C) und höheren Temperaturen (15 °C, 30 °C) als diese Referenz- temperatur gemessen wurden, sind um den Verschiebungsaktor aT, nach rechts bzw. links verschoben. Anders ausgedrückt treten die Relaxationseffekte bei einem Temperaturanstieg schneller auf (zu höheren Frequenzen verschoben). Die Berechnung der Masterkurve und die für das Arrhenius- und WLF-Modell verwendeten Koeffizienten erfolgt automatisch in der rSpace- Software (siehe Tabelle 2).
Zu beachten ist der Frequenzbeginn der Masterkurve: 1.6·10-5 rad/s, das bedeutet mehr als 170 Stunden (mehr als sieben Tage!) nur allein für die Messung eines einzelnen Punkts! Ein solcher Test wäre in der Praxis nicht praktikabel.
Phasenwinkel
Der Phasenwinkel δ (tan δ= G"/G´) ist ein relatives Maß für die viskosen und elastischen Materialeigenschaften. Er reicht von 0° für ein vollständig elastisches Material bis 90° für ein vollständig viskoses Material.
Tab. 2 Arrhenius- und WLF-Koeffizienten, berechnet aus den Messungen für eine Referenztemperatur von 0 °C. Die WLF-Koeffizienten k1 und k2 entsprechen C1 und C2 der WLF-Gleichung; der Arrhenius-Koeffizient k1 dem Faktor E0/R der Arrhenius-Modells.

Tab. 3 Bestimmung des Übergangs der Masterkurve der elastischen und viskosen Schubmodule bei unterschiedlichen Temperaturen

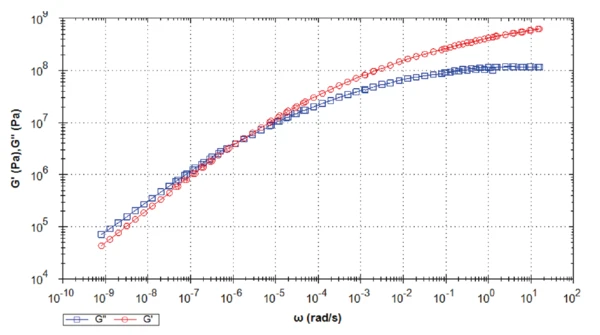
In Abbildung 10 ist die Masterkurve des Asphalt-Bindemittels für eine Temperatur von -30 °C dargestellt. Je niedriger die Temperatur, desto niedriger ist der mittels dieser Berechnung erhaltene Frequenzbereich. Hier liegt der erste Punkt unter 10-9 rad·s-1! Der zwischen 10-7 und 10-6 rad·s-1 Übergang wäre nur durch eine sehr zeitaufwendige Messung detektierbar gewesen.
Tabelle 3 fasst die Ergebnisse der für alle Übergänge zwischen elastischem und viskosem Schubmodul zusammen. Das Asphalt-Bindemittel verhält sich immer wie eine viskoelastische Flüssigkeit für die die vorgegebenen Temperaturen. Je niedriger die Temperatur, umso niedriger ist die Übergangsfrequenz und umso länger dauert der Prozess, der zur Destabilisierung der Materialstruktur führt.
Liegt der Schnittpunkt der G‘- und G‘‘-Kurven bei 2,4∙10-3 Hz bei einer Temperatur von 0 °C, entspricht dies einer Zeitskala von ca. 7 min. Dies heißt, das Material verhält sich überweigend elastisch, wenn die Zeitskala kürzer als 7 min ist. In der Praxis bedeutet dies, dass die Straße bei Belastung innerhalb der Ruhestruktur formstabil ist. Bei längerer Zeitskala steigt die Tendenz, dass sich das Material deformiert (Spurrinnenbildung).
Wird dieses Asphalt-Bindemittel in einem kälteren Klima verwendet, z.B. bei -30 °C, liegt der Schnittpunkt der Kurven G‘ und G‘‘ bei einer niedrigeren Frequenz, d.h. die Zeitskala steigt an (hier ca. 2 Monate).
Zusammenfassung
Das viskoelastische Verhalten von Asphaltbindemitteln wurde zwischen Temperaturen von -30 °C und 30 °C bestimmt. Je niedriger die Prüftemperatur, desto geringer ist die Frequenz des Schnittpunkts. Das Sammeln der Datenpunkte im niederen Frequenzbereich, um den Schnittpunkt erhalten, ist mit sehr langen Messzeiten (mehreren Wochen) verbunden und daher in der Praxis nicht sinnvoll. Mit dem Prinzip der Zeit-Temperatur-Superposition konnte dieses Problem überwunden werden. Anstatt langwierige Tests durchzuführen, wurden Oszillationsmessungen bei fünf verschiedenen Temperaturen über einen üblichen Frequenzbereich durchgeführt. Die daraus resultierenden Grafiken wurden zur Erstellung der Masterkurve herangezogen.