Introduction
The twin dispersion paddle (figure 1) is the right geometry to use for samples that need to be continuously dispersed during the measurement, for example, if pronounced sedimentation on a short-time scale occurs. Because the shear rate applied is not completely uniform, this type of geometry should be considered as a more “relative” geometry giving a good indication of viscosity. On the contrary, a measurement with an absolute geometry as a cone-plate system will lead to the absolute values of the shear viscosity. Here, with this absolute geometry, the shear rate and the shear StressStress is defined as a level of force applied on a sample with a well-defined cross section. (Stress = force/area). Samples having a circular or rectangular cross section can be compressed or stretched. Elastic materials like rubber can be stretched up to 5 to 10 times their original length.stress applied on the sample are clearly defined using the measurement gap with the displacement and the torque, respectively. Measurements carried out on two samples with the same relative geometry can be compared among each other. But it should be kept in mind that they do not provide directly absolute results due to the non-uniform applied shear field. In the following discussion, measurements are performed to demonstrate these differences. To this end, a test done with an absolute geometry is compared to the one carried out with the twin dispersion paddle.

Measurement Conditions
A rotational (viscosity) measurement was carried out on a wall paint with the twin dispersion paddle (relative geometry) and with a cone-plate system (absolute geometry). Table 1 depicts the conditions used for the tests.
Table 1: Measurement conditions
| Sample | Wall paint | |
| Device | Kinexus ultra+ | |
| Geometry | Absolute: CP4/40 (Cone plate, diameter: 40 mm, cone angle: 4°) | Relative: Cup 25 mm, twin dispersion paddle |
| Gap | 146 μm | 5 mm |
| Shear rate | 0.1 to 100 s-1 | |
| Temperature | 25°C | |
For all rheometers, geometry constants are used as conversion factors to take instrument parameters such as torque and displacement and convert them into StressStress is defined as a level of force applied on a sample with a well-defined cross section. (Stress = force/area). Samples having a circular or rectangular cross section can be compressed or stretched. Elastic materials like rubber can be stretched up to 5 to 10 times their original length.stress and shear rate. For the cone and plate, these constants are well defined1. For a novel geometry such as the twindispersion paddle used in this study, a more recent procedure2 is used to generate close agreement to absolute geometry.
1 Macosko CW: Rheology Concepts, Principles and Applications, Wiley-VCH (1992)
2 Duffy JJ, Hill AJ, Murphy SH: Simple method for determining StressStress is defined as a level of force applied on a sample with a well-defined cross section. (Stress = force/area). Samples having a circular or rectangular cross section can be compressed or stretched. Elastic materials like rubber can be stretched up to 5 to 10 times their original length.stress and StrainStrain describes a deformation of a material, which is loaded mechanically by an external force or stress. Rubber compounds show creep properties, if a static load is applied.strain constants for non-standard measuring systems on a rotational rheometer, Appl. Rheol. 25 (2015) 42670.
Measurement Results
Figure 2 displays the resulting curves of both measurements during the steady state viscometry measurement between 0.1 and 100 s-1. The shear viscosity values obtained with the twin dispersion paddle differ by 10 to 15% from the absolute ones coming from the measurement with the cone-plate system. This error is nearly constant along the complete measurement and is expected due to the non-uniform applied shear profile with a non-absolute geometry. It is possible to make a manual adjustment to the geometry constant to minimize this offset; however, this application note is using default values from the discussed method2 to demonstrate the expected differences from using novel and relative geometries.
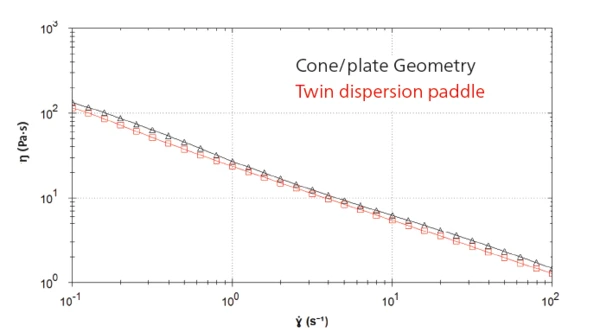
Conclusion
An absolute geometry as the cone-plate geometry system is the first choice to get shear viscosity values. However, if a sample is very unstable, i.e., sedimentation or separation occurs, the use of absolute geometries can be limited, whereas the twin dispersion paddle will give more consistent and representative information about the sample´s viscosity behavior during rheological testing. In this work, it was shown that measurements with the twin dispersion paddle lead to a good approximation of the shear viscosity values of a substance.