Wprowadzenie
Podwójna łopatka dyspersyjna (rysunek 1) jest właściwą geometrią do stosowania w przypadku próbek, które muszą być stale rozproszone podczas pomiaru, na przykład, jeśli występuje wyraźna sedymentacja w skali krótkoterminowej. Ponieważ zastosowana szybkość ścinania nie jest całkowicie jednolita, ten typ geometrii należy uznać za geometrię bardziej "względną", dającą dobre wskazanie lepkości. Przeciwnie, pomiar z geometrią absolutną, taką jak układ stożek-płytka, doprowadzi do bezwzględnych wartości lepkości ścinania. W tym przypadku, przy geometrii bezwzględnej, szybkość ścinania i naprężenie ścinające przyłożone do próbki są wyraźnie zdefiniowane przy użyciu szczeliny pomiarowej odpowiednio z przemieszczeniem i momentem obrotowym. Pomiary przeprowadzone na dwóch próbkach o tej samej geometrii względnej mogą być porównywane między sobą. Należy jednak pamiętać, że nie zapewniają one bezpośrednio bezwzględnych wyników ze względu na niejednorodne przyłożone pole ścinania. W poniższej dyskusji przeprowadzono pomiary w celu wykazania tych różnic. W tym celu test przeprowadzony z geometrią bezwzględną jest porównywany z testem przeprowadzonym z podwójną łopatką dyspersyjną.

Warunki pomiaru
Pomiar rotacyjny (lepkości) przeprowadzono na farbie ściennej z podwójną łopatką dyspersyjną (geometria względna) i z układem stożek-płytka (geometria bezwzględna). Tabela 1 przedstawia warunki zastosowane do testów.
Tabela 1: Warunki pomiaru
| Próbka | Farba ścienna | |
| Urządzenie | Kinexus ultra+ | |
| Geometria | Absolute: CP4/40 (Płytka stożkowa, średnica: 40 mm, kąt stożka: 4°) | Względna: Kubek 25 mm, podwójna łopatka dyspersyjna |
| Szczelina | 146 μm | 5 mm |
| Szybkość ścinania | 0.1 do 100 s-1 | |
| Temperatura | 25°C | |
W przypadku wszystkich reometrów, stałe geometrii są wykorzystywane jako współczynniki konwersji w celu uwzględnienia parametrów przyrządu, takich jak moment obrotowy i przemieszczenie, i przekształcenia ich w naprężenie i szybkość ścinania. W przypadku stożka i płyty stałe te są dobrze zdefiniowane1. W przypadku nowej geometrii, takiej jak łopatka o podwójnej dyspersji zastosowana w tym badaniu, zastosowano nowszą procedurę2 w celu uzyskania ścisłej zgodności z geometrią bezwzględną.
1 Macosko CW: Rheology Concepts, Principles and Applications, Wiley-VCH (1992)
2 Duffy JJ, Hill AJ, Murphy SH: Simple method for determining stress and strain constants for non-standard measuring systems on a rotational rheometer, Appl. Rheol. 25 (2015) 42670.
Wyniki pomiarów
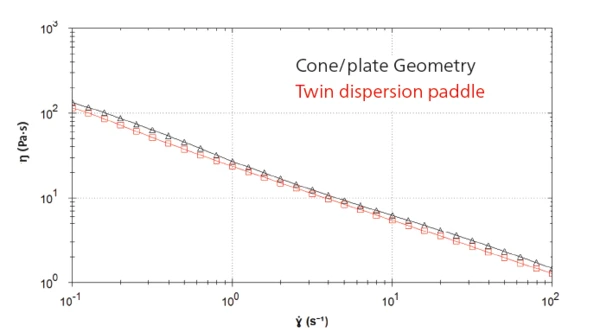
Rysunek 2 przedstawia krzywe wynikowe obu pomiarów podczas pomiaru lepkości w stanie ustalonym w zakresie od 0,1 do 100 s-1. Wartości lepkości ścinania uzyskane za pomocą podwójnej łopatki dyspersyjnej różnią się o 10 do 15% od wartości bezwzględnych pochodzących z pomiaru za pomocą układu stożek-płytka. Błąd ten jest prawie stały podczas całego pomiaru i jest oczekiwany ze względu na niejednolity profil ścinania z nieabsolutną geometrią. Możliwe jest ręczne dostosowanie stałej geometrii w celu zminimalizowania tego przesunięcia; jednak w niniejszej nocie aplikacyjnej wykorzystano wartości domyślne z omawianej metody2,aby zademonstrować oczekiwane różnice wynikające z zastosowania nowej i względnej geometrii.
Wnioski
Geometria absolutna, taka jak system geometrii stożkowo-płytkowej, jest pierwszym wyborem do uzyskania wartości lepkości przy ścinaniu. Jednakże, jeśli próbka jest bardzo niestabilna, tj. występuje sedymentacja lub separacja, zastosowanie geometrii absolutnych może być ograniczone, podczas gdy podwójna łopatka dyspersyjna zapewni bardziej spójne i reprezentatywne informacje o zachowaniu lepkości próbki podczas testów reologicznych. W niniejszej pracy wykazano, że pomiary za pomocą podwójnej łopatki dyspersyjnej prowadzą do dobrego przybliżenia wartości lepkości ścinania substancji.