Introduction
Geometries creating a uniform shear rate profile such as cone/plate and cylindrical systems are preferred for rotational measurements because they lead to absolute values of shear viscosity. The shear rate and shear ContrainteLa Contrainte est définie par un niveau de force appliquée sur un échantillon d’une section bien définie. (Contrainte = force/surface). Les échantillons qui possèdent une section rectangulaire ou circulaire peuvent être comprimés ou étirés. Les matériaux élastiques comme les élastomères peuvent être étirés jusqu’à 5 à 10 fois leur longueur initiale.stress applied on the sample are clearly defined using the measurement gap with the displacement and the torque, respectively.
However, a broad variety of materials cannot be measured with such geometries, for example, if sedimentation occurs or if the sample contains large-sized particles. In these cases, determination of the viscosity is still possible using a “relative” geometry, named as such because the shear rate profile is not entirely uniform.
Figure 1 shows one of these geometries. The twin orbital ball was developed for measurements on building materials that often contain large particles.
Measurements carried out on two samples with the twin orbital ball and the same device can be compared with each other. However, it should be kept in mind that they are not 100% correct due to the non-uniform shear field applied.
In the following discussion, a measurement performed with an absolute geometry is compared to one carried out with the twin orbital ball.

Measurement Parameters
A rotational (viscosity) measurement was carried out on a wall paint with the twin orbital ball (relative geometry) and a cone/plate system (absolute geometry).
The conditions used for the tests are summarized in table 1.
For all rheometers, geometry constants are used as conversion factors, taking instrument parameters such as torque and displacement, and converting them into ContrainteLa Contrainte est définie par un niveau de force appliquée sur un échantillon d’une section bien définie. (Contrainte = force/surface). Les échantillons qui possèdent une section rectangulaire ou circulaire peuvent être comprimés ou étirés. Les matériaux élastiques comme les élastomères peuvent être étirés jusqu’à 5 à 10 fois leur longueur initiale.stress and shear rate. For the cone and plate, these constants are well defined1. For a relative geometry, such as the twin orbital ball, an alternative procedure2 is used to generate close agreement to the absolute geometry.
1 Macosko CW: Rheology Concepts, Principles and Applications, Wiley-VCH (1992)
2 Duffy JJ, Hill AJ, Murphy SH: Simple method for determining stress and strain constants for non-standard measuring systems on a rotational rheometer, Appl. Rheol. 25 (2015) 42670
Table 1: Test Conditions
| Sample | Wall paint | |
| Device | Kinexus ultra + | |
| Geometry | Absolute: CP1/40 (cone plate, diameter: 40 mm, cone angle: 1°) | Twin Orbital Ball |
| Gap | 26 μm | 1 mm (Distance between the balls and bottom of cup) |
| Shear rate | 0.1 to 100 s-1 | |
Measurement Results
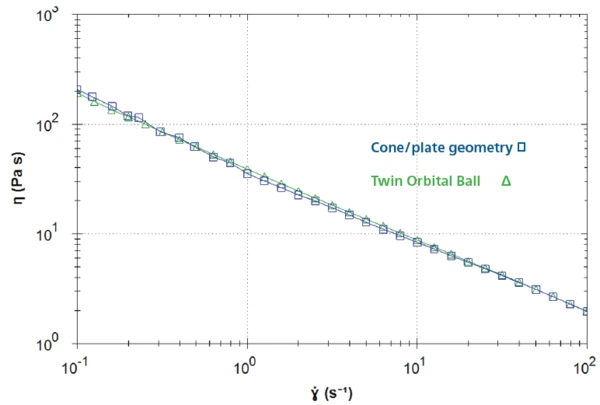
Figure 2 displays the resulting curves of the two measurements during the steady-state viscometry measurement between 0.1 and 100 s-1.
The curves show good agreement between the shear viscosity values obtained with the twin orbital ball and those stemming from the measurement with the cone/plate system over the three decades of shear rate.
Conclusion
An absolute geometry such as a cone/plate geometry is the first choice to obtain shear viscosity values. However, if a sample is very unstable, i.e. sedimentation or separation occurs, or if the sample contains large particles, an absolute geometry is not suitable as shear viscosity values are not representative. The twin orbital ball yields more consistent and representative information about the sample´s viscosity during rheological testing. In this example, it was shown that measurements with the twin orbital ball geometry provide representative shear viscosity values of a material.