Glossary
Payne Effect
The Payne effect is the decrease in the Complex ModulusThe complex modulus consists of two components, the storage and the loss moduli. The storage modulus (or Young’s modulus) describes the stiffness and the loss modulus describes the damping (or viscoelastic) behavior of the corresponding sample using the method of Dynamic Mechanical Analysis (DMA). complex modulus of a filled, crossed-linked elastomer system with increasing deformation amplitude.
If the sample is deformed sinusoidally, the StrainStrain describes a deformation of a material, which is loaded mechanically by an external force or stress. Rubber compounds show creep properties, if a static load is applied.strain follows the StressStress is defined as a level of force applied on a sample with a well-defined cross section. (Stress = force/area). Samples having a circular or rectangular cross section can be compressed or stretched. Elastic materials like rubber can be stretched up to 5 to 10 times their original length.stress with a time delay. The decrease in the shear modulus shows a non-linear behavior and can essentially be attributed to the so-called filler-filler interaction (see Figure 1). Different effects contribute to the overall strength of the elastomer:
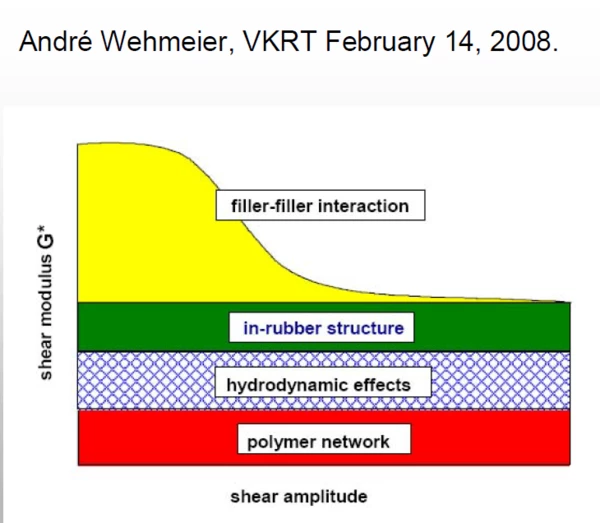
Modulus of the unfilled rubber network
The contribution of the rubber matrix of the (unfilled) rubber network to the total stiffness is independent of the amplitude.
Hydrodynamic effect of filler particles
Hydrodynamic effect of the filler particles (e.g. due to large Carbon BlackTemperature and atmosphere (purge gas) affect the mass change results. By changing the atmosphere from, e.g., nitrogen to air during the TGA measurement, separation and quantification of additives, e.g., carbon black, and the bulk polymer can become possible.carbon black particles N8 … N9):
The inelastic filler particles do not participate in elongation and cause higher intrinsic polymer StrainStrain describes a deformation of a material, which is loaded mechanically by an external force or stress. Rubber compounds show creep properties, if a static load is applied.strain compared to the applied macroscopic StrainStrain describes a deformation of a material, which is loaded mechanically by an external force or stress. Rubber compounds show creep properties, if a static load is applied.strain. This effect depends on the volume filling level, but is independent of the load amplitude and is a significant contribution to the overall stiffness.
In-rubber structures
There are filler/matrix interactions (e.g. due to small to medium filler clusters with N1…, N2..., to N5…)
Filler-matrix interactions:
Parts of the rubber are immobilized in the filler structure. This immobilization also contributes to the overall stiffness independent of the amplitude.
Filler-filler Interactions
The filler-filler interaction is essentially responsible for the decrease in the modulus. Due to the mechanical load, the Carbon BlackTemperature and atmosphere (purge gas) affect the mass change results. By changing the atmosphere from, e.g., nitrogen to air during the TGA measurement, separation and quantification of additives, e.g., carbon black, and the bulk polymer can become possible.carbon black agglomerates (clusters) are broken, resulting in a decreasing stiffness. Active Carbon BlackTemperature and atmosphere (purge gas) affect the mass change results. By changing the atmosphere from, e.g., nitrogen to air during the TGA measurement, separation and quantification of additives, e.g., carbon black, and the bulk polymer can become possible.carbon black or silica can form a filler-filler network within the polymer matrix, offering high resistance to the small amplitudes. If the amplitude gets too large, this network breaks down and as a result, the G* modulus decreases drastically. For large deformations, the contribution of the filler-filler network to the Complex ModulusThe complex modulus consists of two components, the storage and the loss moduli. The storage modulus (or Young’s modulus) describes the stiffness and the loss modulus describes the damping (or viscoelastic) behavior of the corresponding sample using the method of Dynamic Mechanical Analysis (DMA). complex modulus virtually disappears.
The decrease in the modulus is non-linear. This non-linearity is due to hysteresis losses, occurring during degradation of the filler network as well as the release of the polymer trapped in the filler network, which can then contribute to the elongation again.

