24.01.2023 by Rüdiger Sehling
New Possibilities with the NETZSCH DMA Calculator
About the Influence of the Entered Sample Geometry on the Elasticity Modulus in Bending Mode ‒ New Possibilities with the NETZSCH DMA Calculator
Dynamic mechanical analysis (abbreviated: DMA) is a method that provides information on the elastic and viscous behavior of a material as a function of temperature, time and load frequency.
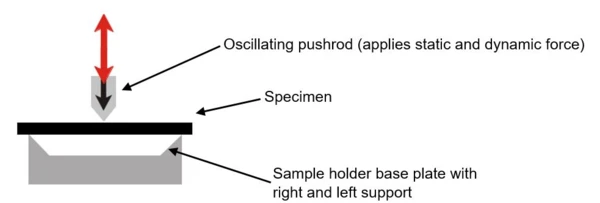
The bending setup is the most common measurement type for DMA systems. In this setup, very stiff and hard samples (e.g., metals, fiber-reinforced and highly filled thermosets) as well as thermoplastics can be measured. For example, in 3-point bending mode, a specimen is placed on the right and left support in a free position without clamping. The pushrod applies the oscillating load from the top. This setup consequently allows for the modulus values to be measured very precisely.
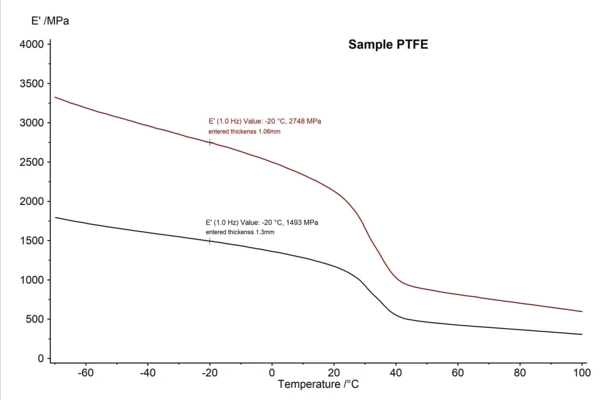
Generally, it is important to have exactly defined specimen geometries because even small tolerances generate significant differences in the modulus values, especially for thin samples. In bending mode (3-point bending and dual or single cantilever), the entered sample thickness is included to the 3rd power in the calculation of the modulus. This means plane-parallel surfaces are very important in order to measure reliable modulus values. If this is not the case, differences in the modulus result from only slightly different specimen geometries. Especially for thin sample strips, differences in thickness can very often be measured. In figure 2, the example of a PTFE strip demonstrates that the thickness varies from 1.06 mm to 1.3 mm.

In figure 3, the DMA measurement results for the PFTE strip are shown in a temperature range from -70°C to 100°C. In order to demonstrate the influence of different sample geometries, for the 1st test (black curve), a sample thickness of 1.3 mm was entered, and for the 2nd test, a thickness value of 1.06 mm. When comparing the two measurements, it can be seen that the measured modulus values deviate greatly from one another across the temperature range (by approx. 84%, evaluated for example at -20°C).
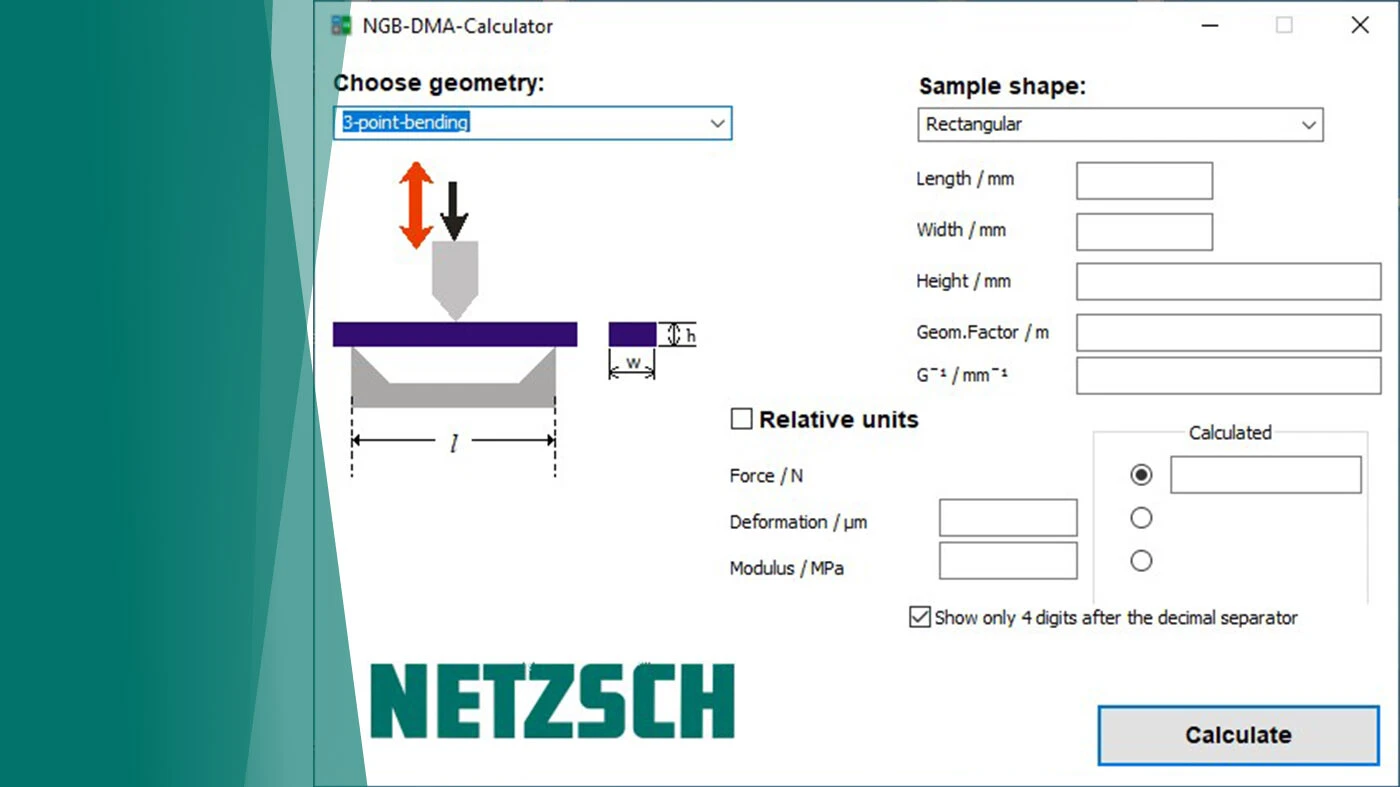
The DMA Calculator shows results quickly
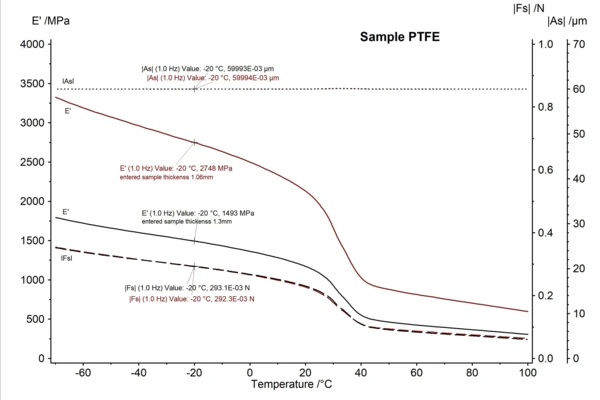
This influence of the specimen thickness can also easily be demonstrated with the DMA calculator (included in the NETZSCH Proteus® software), with which modulus, deformation and force values can be calculated. For calculation of the modulus values, it is generally necessary to know the value for the dynamic force and also for the dynamic amplitude. From these two values, the stiffness of a material is calculated; this is then multiplied by a geometrical factor in order to calculate the modulus. The values for the dynamic force and dynamic amplitude can easily be evaluated in the Proteus® software. In figure 4, the signals of the dynamic force IFsI and dynamic amplitude IAsI are additionally shown for the PTFE specimen measured. It can be seen that the values for the dynamic force and dynamic amplitude are nearly identical for the two measurements (black and brown), which also demonstrates the high reproducibility of the NETZSCH DMA. This means that the measured modulus value only depends on the geometry entered. These evaluated values for the dynamic force IFsI and dynamic amplitude IAsI can now be used for the DMA calculator to check the influence of slightly different values in entered sample geometries.
DMA calculator – How to use this tool to check the influence of different entered sample thicknesses on the calculated modulus, demonstrated with the example of PTFE:
Specified sample thickness: 1.3 mm
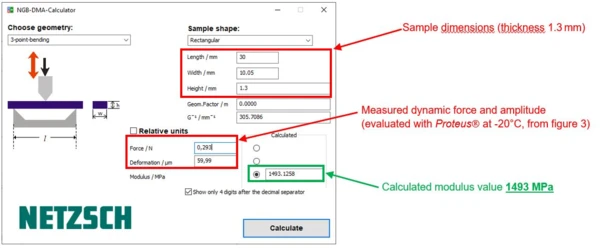
On the same specimen, only the sample thickness was changed from 1.3 mm to 1.06 mm to see the influence:
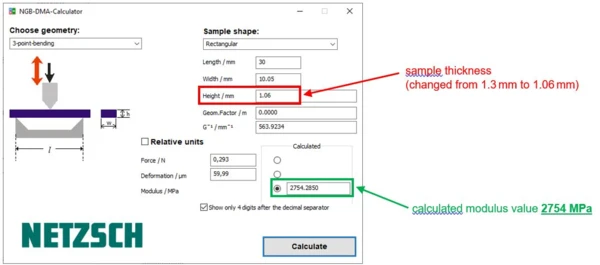
DMA Calculator - Lots of Advantages
By means of the DMA calculator, it can be quickly illustrated that differences in sample thickness generate significant differences in the modulus value (here 1493 MPa to 2754 MPa -> approx. 84% deviation at -20°C). This example shows again that differences in the measured modulus E’ can result from slightly different determined sample thicknesses although the sample material is identical. To estimate and show this influence, one can simply use the DMA calculator. Thus, it is no longer necessary to perform multiple DMA measurements to demonstrate this influence. As shown in the example, the tolerance range of the modulus value can now easily be estimated for each individual measurement.
A further advantage is that the DMA calculator can be used for any DMA measurement type: 3-point bending, single/dual cantilever, tension, compression, penetration or shearing. Furthermore, with this DMA calculator, it is also possible to calculate forces and amplitudes for a given material in advance in order to find a suitable measurement setup as well as suitable sample geometries.
The DMA calculator is a flexible and unique tool for the quick calculation of all relevant DMA measurement values, serving both for better interpretation of the results and for finding the best measurement setup for the respective material.
Learn more about the basics and application areas of Dynamic-Mechanical Analysis:
Register for our webinar on February, 14!
The webinar is an introduction to the DMA method and is primarily aimed at beginners. Content of this webinar is the explanation of the viscoelastic material behavior, the basics of the DMA measurement technique of DMA along with selected material properties based on application examples.




