Introduction
Quartz, also called low-temperature quartz or α-quarz, is a mineral with the chemical composition SiO2 and trigonal symmetry. On the Earth’s surface, it is the stable form of silicon dioxide and one of the most common minerals in the continental crust. It occurs as a rock-forming material in both the mantle and crust of the Earth. [1]
Quartzous subsurface materials affect tectonic behavior as they carry seismic waves according to their dynamic mechanic and thermal properties [2].
At 573°C and under normal pressure, the low-temperature modification changes from trigonal to hexagonal (high-temperature modification). This change in modification is displacing, very fast and reversible. During this process, physical properties (volume, Thermal ConductivityThermal conductivity (λ with the unit W/(m•K)) describes the transport of energy – in the form of heat – through a body of mass as the result of a temperature gradient (see fig. 1). According to the second law of thermodynamics, heat always flows in the direction of the lower temperature.thermal conductivity, dynamic-mechanic parameters, etc.) change significantly, allowing this transformation temperature to be used for temperature calibration. [3]
Another characteristic of quartz is its resistance to oxygen up to high temperatures. This is an appreciated property that simplifies handling in practice. Purge gases are not required. [4]
Natural quartz crystals consist of Si and O2, which form links of [SiO4]4 tetrahedra. Other elements are only present in traces in the crystal lattice.
Quartz single crystals feature distinctive anisotropy in optical and mechanical elastic properties, among others. If, however, a material consists of a variety of differently oriented individual crystals, anisotropy weakens considerably with less pronounced preferred orientation of the individual crystallites. Many transitional forms occur between macroscopically isotropic quartz multicrystals and strongly anisotropic synthetic single crystals. The spectrum ranges, for example, from amorphous silica glass (= quartz glass) to sandstone [quartz content above 50% and quartzites NOT bound by SinteringSintering is a production process for forming a mechanically strong body out of a ceramic or metallic powder. sintering (rocks with high quartz content of ≈98%+, but sintered quartz crystals)], and from rock crystal as the natural version of the single crystal to synthetic quartz single crystal, which are widely used.
For example, quartz single crystals have long been used as oscillating crystals (timers) or igniters due to their piezo-electric and optical properties. In microelectronics, quartz crystals have been applied as dielectric layers in transistors, capacitors, and hard masks in photolithography, and additionally as micro-electro mechanical systems (MEMS) for industrial and biomedical applications. [5]
For the use of strongly anisotropic quartz single crystals for temperature calibration in the high-temperature DMA (HT Eplexor®), some precautions are necessary due to the distinct anisotropy. The naturally increasing thermal expansion during a temperature sweep (e.g., temperature ramp at 10 K/min) leads to internal mechanical stresses in the quartz. If the quartz sample is additionally exposed to a temperature gradient within the measuring chamber (HT furnace), these internal stresses will inevitably lead to cracking or breakage of the sample. It is therefore necessary to keep the temperature gradient in the furnace as low as possible by taking suitable measures.
The HT Eplexor®, equipped with a separated sample chamber and an additional temperature shield, meets these requirements. Thus, the phase transformation at 573°C can even be run several times on the same sample without destroying the sample due to the temperature gradient. One of the constructive measures is demarcation of a region in the furnace chamber with a good heat-conducting cylindrical protective shield around the sample.
Experimental



Without these additional measures to reduce thermal gradients, self-destruction of the quartz wafer specimen takes place regularly even without an applied test load (figure 1). This is caused by temperature gradients that are too large in the sample range.
For homogenization of the temperature distribution and for reduction of the temperature gradient in the specimen, a cylindrical temperature shield made of copper is used (figure 2, left), which encloses the sapphire bending holder (left) and the piston acting gimbally on the specimen (figure 2, right) at half height. The force axes built into the HT Eplexor® consist of polycrystalline Al2O3.
The force axes are designed as 3-point bending holders (bearing distance here 20 mm). As the sample support system, a cuboid sapphire carrier with a width of 15 mm, a height of 7 mm and a length of approx. 50 mm is used. On the upper side of the carrier, two sapphire rollers support the samples at predefined positions are very well suited. The distance between the rollers can thus be selected in steps of 5 mm, allowing 3-point bending supports to be spaced from 10 to 35 mm apart. The third sapphire roller is placed centrally on the upper side of the sample as a compression die (figure 2, right). The rollers are 15 mm long and have a diameter of 4 mm. The roller bearing prevents significant tensile loads during deflection while the gimbal bearing in the piston always ensures line contact between the piston and sample.
Using a T shield and the „gimbal roller bearing“ (figure 3), self destruction does not occur, even under test load (Fstst = 0.25 N, Fdyn = 0.15 N). This also applies for multiple runs (heating/cooling) of the α/β transition.
Under such experimental conditions, temperature sweeps spanning the temperature range of the α/β transition can successfully be carried out on quartz wavers. After completion of the measurements, the sample can be removed without damage.
Measurement Results
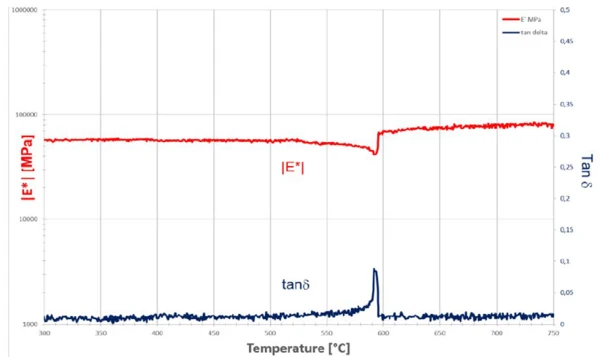
The a/ß Phase TransitionsThe term phase transition (or phase change) is most commonly used to describe transitions between the solid, liquid and gaseous states.phase transition of quartz crystals can, for the first time, be reliably detected mechanically with the help of the high-temperature DMA in the form of a temperature sweep (figure 4). Determination of the transition temperature can be made based on the temperature dependence of the Young’s modulus |E*| and/or damping (tan δ). Thus, the temperature prevailing at the sample location is also known and can be used as a calibration standard.
In theses investigations, the focus was on the recording of the behavior close to the α/β transition. To this end, low test loads (here Fstatic = 0.25 N, Fdynamic = ± 0.15 N) and low heating rates (2 K/min) must be applied.
The HT Eplexor® is very well suited for carrying out such dynamic-mechanical investigations due to its ability to select load cells of suitable nominal load for to the casespecific requirements.
Summary
The loads adapted to the material behavior in the temperature range around 550°C prevent sufficiently good coupling of the sample to the bending support at lower temperatures. The result is an underestimated Young’s modulus |E*| in the RT range. Good coupling requires, for sample dimensions of 1.03 mm x 10.81 mm x 35 mm, static forces of at least 5 N and separate measurements. If these loads were applied in the temperature range of the α/β transition, destruction of the sample would have inevitably occurred. Therefore, a load reduction was carried out here at higher temperatures.