Starting Position
Quite a few ceramic materials (monolithic ceramics) break under the influence of even low mechanical loads. A typical test geometry for determining the strength of ceramics (complex modulus of elasticity and damping tan δ) is known as 3-point bending.
In this case, a strip specimen with dimensions of, for example, 30 mm x 5 mm x 1 mm is usually placed on a U-shaped support with a flank spacing of, for example, 20 mm and is mechanically “loaded” or “bent” in the center by means of a push rod.
Embedding fibers in a monolithic matrix leads to socalled ceramic matrix composites (CMCs). Under load, the ceramic matrix forms initial cracks during the manufacture of the composite. These cracks, however, are bridged by load-bearing fibers, so the material does not break and is more damage-tolerant.
If the fiber/matrix composite is not particularly strong, significantly higher elongations up to fiber fracture elongation (usually <3%) can be realized in the composite before final breakage occurs. Compared to the elongation at break of metals and polymers, that of fiber ceramics still remains small.
For dynamic-mechanical analysis of monolithic ceramics and fiber ceramics, this means that small deformations must be recorded and evaluated up to high temperatures.
At the same time, 3-point bending tests do not represent a physically clean load state due to the tensile, compression and shear components occurring as a result of the test geometry. They are therefore always a compromise. More appropriate tensile tests fail due to the lack of suitable clamping possibilities for brittle ceramic materials that are thus easily broken. Therefore, the method of choice remains the 3-point bending test.
A stable frictional connection between the sample holder and sample, which ideally does not change for the duration of the analysis, is absolutely necessary. The frictional connection is insufficient, for example, if the sample geometry deviates from plane parallelism and the two supports are only partially in contact with the sample.
Also, different coefficients of thermal expansion (Coefficient d'Expansion Thermique Linéaire (CLTE/CTE)The coefficient of linear thermal expansion (CLTE) describes the length change of a material as a function of the temperature.CTE) of the sample and the fixed bending support lead to undesired mechanical stresses in the sample’s longitudinal direction due to friction between the support and the sample. These are superimposed on the mechanical ContrainteLa Contrainte est définie par un niveau de force appliquée sur un échantillon d’une section bien définie. (Contrainte = force/surface). Les échantillons qui possèdent une section rectangulaire ou circulaire peuvent être comprimés ou étirés. Les matériaux élastiques comme les élastomères peuvent être étirés jusqu’à 5 à 10 fois leur longueur initiale.stress applied, thus falsifying the measurement results.
In addition, inner thermal stresses occurring even without mechanical load can cause mechanical destruction of sensitive samples due to temperature gradients in the furnace (example: quartz wafers). The objective is to reduce all these interference effects.
Experimental Solutions
Constructive measures are used to counteract the afore-mentioned interference effects.
Homogenization of the Temperature in the Sample Region
Two different solutions are used as measures for temperature homogenization.
Fiber-Ceramic Furnace Inset (Figure 1)
This is a fiber-reinforced oxide ceramic separating the sample and furnace chambers and reducing temperature gradients. In addition, this insert offers the ability to realize oxygen-low or, if required, other gas atmospheres inside.
As an additional component, a thermal protective shield (figure 2) can be used in conjunction with the furnace insert or separately. The thermal protective shield (figure 2) can be placed on top of the bending support in order to reduce thermal gradients inside and thus in the sample’s proximity.
The simple Cu version can be used up to max. 950°C. Above that temperature, a zirconium version should be used. Both versions are wear parts, so-called “sacrificial” materials, as they are slowly consumed by OxidationOxidation can describe different processes in the context of thermal analysis.oxidation.
The effect of the disturbing differences in the coefficients of thermal expansion can be eliminated by a bending support with roller bearings (sapphire). The polished sapphire bending support (figure 3) is not subject to any Phase TransitionsThe term phase transition (or phase change) is most commonly used to describe transitions between the solid, liquid and gaseous states.phase transitions across the entire relevant temperature range. Due to its single crystal structure, it has relatively few spots capable of reaction, i.e., it is chemically inert. For these reasons, sapphire is perfect for use as a bending support! The polished rollers, which are also made of sapphire, compensate for the different thermal expansions by converting the thermal deformation difference between the sample and support into a rotational movement. The change in span thereby occurring in principle is only marginal. If a chemical material incompatibility between the rollers and sample occurs, the damage can easily be repaired. The rollers are designed as wear parts and can therefore easily and quickly be replaced. Different roller materials are available as an alternative (e.g., Si3N4 and SSiC rollers).
For optimization of the mechanical coupling, a gimbally mounted support (figure 3, top center) can be employed. This push rod primarily serves for compensation of the lacking plane parallelism of the sample. It is, however, also effective in the case of a Thermally induced reactionA thermally induced reaction is a decomposition reaction exclusively started through heat treatment. thermally induced twist of the sample by virtue of always adjusting the gimbal support to the respective surface.



Measurement Results
The temperature sweep carried out under the application of these constructive improvements on
a) a polycrystalline Al2O3 sample (figure 4),
b) a sapphire sample, also an Al2O3 single crystal (figure 5) and
c) a C/CSiC composite (figure 6)
yield the following results:
a) Polycrystalline Al2O3
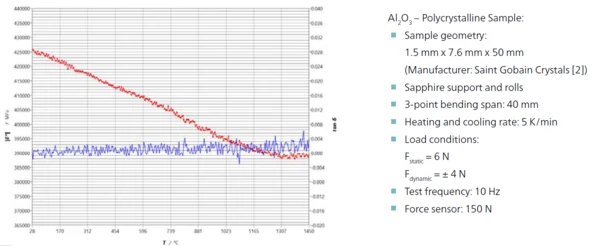
The two Al2O3 materials investigated are fundamentally different in structure. The polycrystalline Al2O3 sample consists of α-Al2O3 of a purity of 99.7% and is sintered. It has a glass phase surrounding the individual crystallites. At temperatures above approx. 1100°C, this intercrystallite glass phase begins to soften [2], which is expressed as a creeping process in the temperature sweep (figure 4) and is characterized by a sharp drop in the Young’s modulus.
b) Sapphire (Single Crystal)
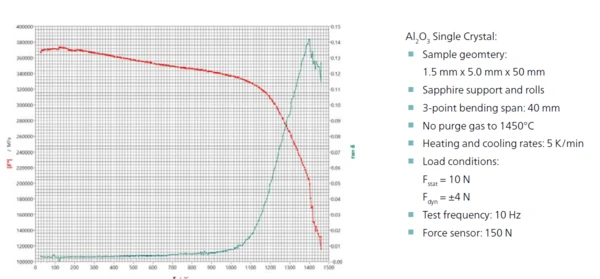
In the case of the sapphire single crystal, structural relationships are completely different. In a single crystal, of course, there are no grain boundaries and glass phases. Thus, it is also free of creep effects, but also much less tolerant to damage. The continuous drop in |E*| and the absence of any signs of creep effects are to be expected, as are the lower damping values in comparison with to the polycrystalline sample (figure 5).
c) C/SiC Fiber Ceramic
C/SiC composites, manufactured by the University of Queensland, present an example for the use of a fiber ceramic in the HT DMA. This is a composite manufactured by the polymer infiltration process (PIP) with preceramic precursor which was then subjected to a PyrolysisPyrolysis is the thermal decomposition of organic compounds in an inert atmosphere.pyrolysis process (1600°C) under an argon atmosphere. This 20-layer composite has a layer-by-layer unidirectional fiber arrangement with an alternating 0°/90° arrangement and a fiber volume fraction of approx. 50% [1].
The dynamic-mechanical investigation was carried out under surrounding-atmosphere conditions in a (heating) temperature sweep from room temperature to approx. 1300°C, followed directly by another temperature sweep from 1300°C to room temperature. The heating and cooling rates amounted to 10 K/min. For measurement data acquisition, a static force of 55 N is first applied to excite the sample (12.8 mm x 4.5 mm x 50 mm; span 44.5 mm) with a dynamic superimposed force of the amplitude of 45 N at a test frequency of 3 Hz. The measurement result is shown in figure 6.
While for unreinforced ceramics such as SiC, the Young’s modulus decreases with temperature [3], C/SiC fiber ceramics show an increasing Young’s modulus. RFDA measurements (Resonant Frequency Damping Analysis) by DLR Stuttgart [4] on C/SiC fiber ceramics provide the same finding. The DLR results also show an increasing Young’s modulus with rising temperature. Normally, a modulus increase with temperature is not expected and therefore somewhat surprising.
In fiber ceramics, however, microstructural causes can explain the increase in Young’s modulus in C/SiC composites due to heating. Among other things, PyrolysisPyrolysis is the thermal decomposition of organic compounds in an inert atmosphere.pyrolysis yields a material that is already cracked at room temperature and under internal stresses because of the mass losses in the matrix portion. With increasing temperature, the cracks close again, i.e., the force flow increasingly occurs directly via the matrix due to the greater expansion of the same.
The image of deformation artefacts, which have their origins in the contact area between the sample and the bending holder and can be eliminated by rollers and gimbal bearing, must be extended into the material for fiber ceramics. Fiber ceramics, such as C/SiC, are subject to cracking due to the manufacturing process. It is likely that the cracks, which become wider at lower temperatures and narrower with increasing temperature, cause less intrinsic deformation due to the thermal expansion. Further investigations are planned.
The thermal expansion of the matrix – which is usually greater than that of the fiber content – then causes the cracks inherent in the samples, which are also of differing widths, to initially reduce in size with increasing temperature and then possibly even close.
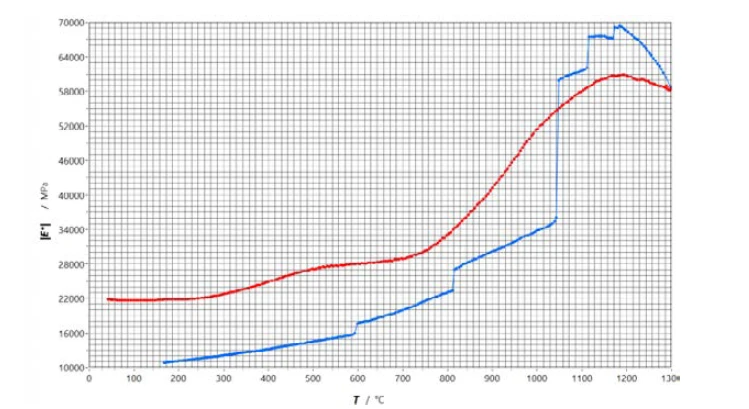
With increasing temperature, the overestimation of the deformation decreases, so Young’s modulus increases. The true temperature-dependent behavior of the cracked material is thus reflected in Young’s modulus! In ambient atmosphere, OxidationOxidation can describe different processes in the context of thermal analysis.oxidation at the crack surface can also damage fibers. Such consequences become visible after prolonged exposure through a repeated decrease in the moduli, mainly during cooling. The cracks already enlarged by previous OxidationOxidation can describe different processes in the context of thermal analysis.oxidation broaden further during cooling. If the oxidative damage leads to cracks in the fiber segments, these can be seen as jumps in the Young’s modulus course.
Summary
Dynamic-mechanical analysis (DMA) can reliably and relatively quickly determine elastic properties such as Young’s modulus |E*| and damping tan δ under application-proximate conditions with the design modifications presented. Temperatures to 1500°C are possible, as is the selection of the atmosphere in the sample chamber (e.g., surrounding conditions, inert gas or low-oxygen environment). This also applies for fiber ceramics such as C/SiC. The designer thus obtains temperature-dependent mechanical data up to 1500°C for the design of fiber-ceramic (structural) components under application conditions. By changing the working atmosphere in the sample chamber, it is also possible to change the rate of damage due to OxidationOxidation can describe different processes in the context of thermal analysis.oxidation in a targeted manner.