Introduction
An emulsion is a system with a liquid continuous phase and a dispersed phase of liquid droplets. The two types of emulsions which are most common are oil-in-water emulsions and water-in-oil emulsion (Figure 1). In an oilin- water emulsion, the continuous phase is water and the dispersed phase is oil, while in a water-in-oil emulsion, the continuous phase is oil, while the dispersed phase is water.
Whether a water-in-oil emulsion turns into an oil-inwater emulsion depends upon the volume fraction of both phases and the emulsifier. An emulsifier is a material that stabilizes an emulsion by adsorbing at the oil/ water interface. Surfactants are the most common form of emulsifier although polymeric and particulate materials can often fulfill a similar role.
Emulsion rheology tends to have a very strong dependence on the volume fraction of the dispersed phase as well as the droplet size. The rheological parameters of key interest are the viscosity, Normal stress, viscoelasticity and the Yield StressYield stress is defined as the stress below which no flow occurs; literally behaves like a weak solid at rest and a liquid when yielded.yield stress.
The relative viscosity of a dilute emulsion with a low Capillary number (so that the droplets do not deform) is given by the following expression [1]:
and ηd is the dispersed phase viscosity and ηs is the viscosity of the suspending fluid. Here, it is assumed that the emulsion is not shear thinning, hence the viscosity will be the same at each shear rate. For higher droplet concentrations (Φ≥0.6), the system becomes shear thinning and the relative zero shear viscosity is then given by the following expression:
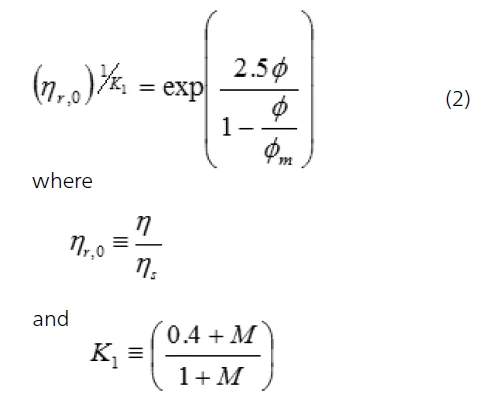
Φm is the maximum packing fraction.
The shear thinning becomes more pronounced as volume fraction of droplets increases. In reference [2], this is accounted for by adjusting Φm to get a best fit at each shear rate.
With a further increase in volume fraction, a situation may be reached where droplets become jammed, thus preventing particles moving relative to one another. It is in this situation that the system is considered to have a Yield StressYield stress is defined as the stress below which no flow occurs; literally behaves like a weak solid at rest and a liquid when yielded.yield stress. This is discussed in a separate application note.
Note also that this associated theory assumes a simple emulsion and does not account for the presence of rheology modifiers such as cross-linked micro-gels for example which have considerable phase volume and will significantly impact the solvent and hence emulsion rheology.
To experimentally verify this theory for a given emulsion system, it is necessary to determine the zero shear viscosity of an emulsion at various droplet concentrations and then calculate zero shear relative viscosity for each concentration using the viscosity of the suspending media. The plotted relationship between the zero shear relative viscosity and the concentration should indicate whether or not the above theory approximates the behavior of the emulsion system being studied. The data can be further extracted and analyzed to investigate exact fit with the above models. The same sequence can also be utilized to investigate the impact of changing the droplet size on the viscosity.
Experimental
- This test exists as a pre-configured sequence in the rSpace software which is designed to run on a Kinexus rotational rheometer1.
- The sequence runs a table of shear stresses and then fits an Ellis Model to the data to determine η0 and then ηr,0
- This is repeated for a number of concentrations and a plot of ηr,0 against concentration is obtained, which can be subsequently exported and analyzed outside of the software.
Please note...
that a parallel plate geometry or a cylindrical geometry can also be used. A sand blasted geometry should be considered if the material is likely to show wall slip effects. Larger geometries are useful for measurements at low torques, which are more likely to be encountered at lower frequencies. The use of a solvent trap is also recommended for these tests since evaporation of solvent (e.g., water) around the edges of the measuring system can invalidate the test, particularly when working at higher temperatures.