Introduction
Die Lebensdauer eines Asphaltbindemittels steht in engem Zusammenhang mit seinen viskoelastischen Eigenschaften. Eine einfache Möglichkeit zur Bestimmung dieser Eigenschaften ist die Durchführung von Frequenz-Sweep-Messungen mit einem Rotationsrheometer. Der niedrige Frequenzbereich eines solchen Tests entspricht langen Zeitskalen, während der höhere Bereich Informationen über das Verhalten der Proben in kurzen Zeitskalen liefert.
In der Praxis stellt die Durchführung von Tests bei sehr niedrigen Frequenzen oft eine Herausforderung dar, da sie mehrere Tage oder Wochen in Anspruch nehmen kann. Dennoch ist es wichtig, das Verhalten von Bitumen oder Asphaltbindemitteln über längere Zeiträume vorherzusagen.
Wie lässt sich das Langzeitverhalten von Asphaltbindemittelnvorhersagen?
Die Antwort liefert die Zeit-Temperatur-Superposition (engl. Time-Temperature Superposition, TTS). Dieses Prinzip beruht auf der Tatsache, dass eine Temperaturverschiebung die gleichen Auswirkungen auf die viskoelastischen Eigenschaften hat wie eine Frequenz- oder Zeitverschiebung. Mit anderen Worten: Sie können den Frequenzbereich einer Messung erweitern, indem Sie Tests im gleichen Frequenzbereich, jedoch bei unterschiedlichen Temperaturen durchführen.
Wie wird die Zeit-Temperatur-Superposition angewandt?
Ziel ist es, die Ergebniskurven eines Frequenz-Sweeps auf einen breiteren Frequenzbereich auszudehnen. Die Methode ist einfach:
- Frequenz-Sweep-Messungen bei unterschiedlichen Temperaturen.
- Erstellung einer Masterkurve bei einer anwenderdefinierten Temperatur. Die Sequenz zur Erstellung einer Masterkurve ist in der rSpace-Software1 integriert.
Beispiel: Erstellung einer Masterkurve für ein unmodifiziertesAsphaltbindemittel
An einem unmodifzierten Asphaltbindemittel werden bei unterschiedlichen Temperaturen Frequenz-Sweeps durchgeführt. Tabelle 1 fasst die Messbedingungen zusammen.
Linear viskoelastischer Bereich
Der LVR ist der Amplitudenbereich, in dem Deformation und Schubspannung proportional sind. Im LVR reichen die angewandten Schubspannungen (oder Deformationen) nicht aus, um einen strukturellen Zusammenbruch zu verursachen, und daher werden die mikrostrukturellen Eigenschaften gemessen.
Tab.1 Messbedingungen
| Gerät | Kinexus DSR-III | |||||
| Geometrie | Platte-Platte, Druchmesser: 8 mm | Platte-Platte, Durchmesser: 25 mm | ||||
| Messspalt | 2 mm | 1 mm | ||||
| Temperatur | 5 °C | 15 °C | 25 °C | 35 °C | 45 °C | 65 °C |
| Scheramplitude | Bestimmt, um im LVR-Bereich zu liegen | |||||
| Frequenz | 0,01 bis 40 Hz2 | |||||
1 Die Kinexus Prime DSR-Software enthält sowohl Mess- als auch Auswerteroutinen
2 begrenzt durch die Trägheit der Apparatur
Messergebnisse
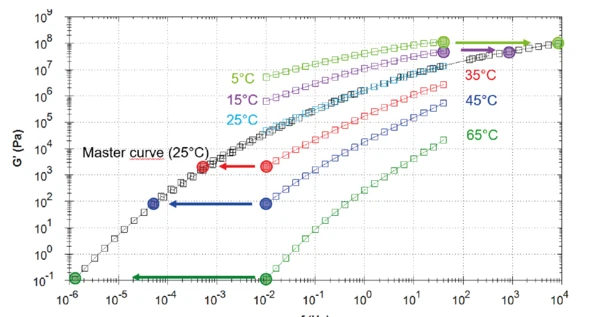
Abbildung 1 zeigt den elastischen Schubmodul (G') für die verschiedenen Prüftemperaturen (farbige Kurven). Je höher die Temperatur, desto geringer ist der elastische Schubmodul. Das bedeutet, dass das Material mit steigender Temperatur bei einer festen Frequenz an Elastizität verliert. Bei 0,01 Hz steigt der Elastizitätsmodul von 1E-01 Pa bei 65 °C auf fast 1E+07 Pa bei 5 °C an, ein Unterschied von nahezu 8 Dekaden! Dieser starke Temperatureinfluss erklärt auch die jahreszeitlich bedingten Schwankungen der Asphalteigenschaften. Im Winter können die Straßen spröde sein und zu Rissen neigen, während sie in sehr heißen Sommern klebrig werden können. Aus diesem Grund werden verschiedene Bindemittelqualitäten entwickelt, um den unterschiedlichen Bedingungen je nach Land, Staat/Region und Nutzung (z.B. Landstraße vs. Autobahn) Rechnung zu tragen.
Die Masterkurve bei einer Referenztemperatur von 25 °C (schwarze Kurve) ergibt sich aus der Verschiebung der Messpunkte der Frequenz-Sweeps (siehe Beispielpunkte in Abbildung 1). Je höher die Temperatur, desto flexibler sind die Polymerketten und desto mobiler sind die Moleküle. Daher ist der Relaxationsprozess, der bei niedriger Temperatur und niedriger Temperatur stattfindet, bei höherer Temperatur und höherer Frequenz derselbe.1
Die bei einer Referenztemperatur von 25 °C erhaltene Masterkurve erstreckt sich von 1E-06 bis 1E+04 Hz, also besteht eine Erweiterung des Frequenzbereichs um fast 7 Dekaden! Eine Frequenz von 1E-06 Hz entspricht mehr als 11 Tagen. Eine solche Dauer für die Messung nur eines Punktes ist in der Praxis nicht zweckdienlich, was die TTS absolut notwendig macht.
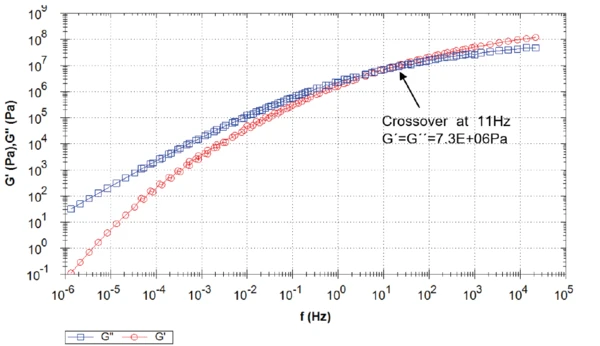
In Abbildung 2 ist die Masterkurve bei 25 °C für den elatischen (G´) und Verlust-Schubmodul (G") dargestellt. Sie zeigt, dass sich Kurven von G´ und G" bei 11 Hz kreuzen, was bedeutet, dass das Bindemittel bei Zeitskalen von weniger als 90 ms elastisch dominiert wird. Diese Periodendauer entspricht dem Start des Fließens bei jeder Belastung für diese Temperatur.
1 Weitere informationen über die Abhängigkeit der Relaxationszeit von der Temperatur sind in unserer Application Note 256 (Time-Temperature Superposition an Asphaltbindemittel) zu finden.
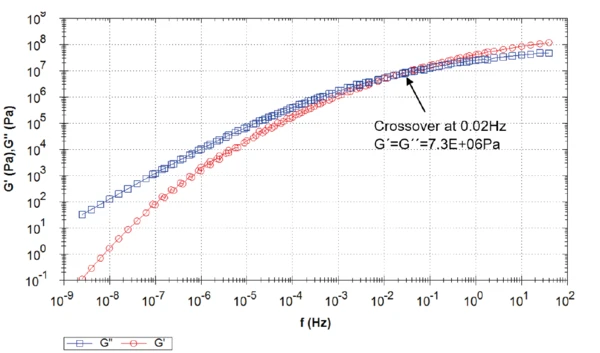
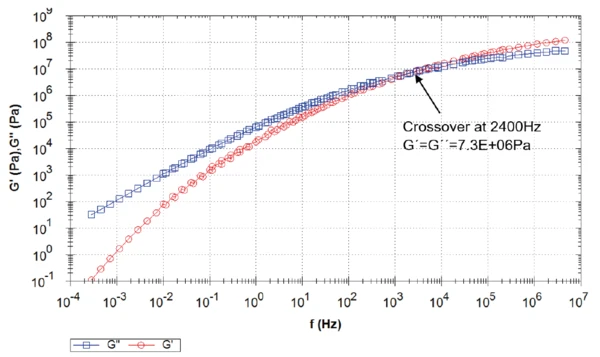
Zum Vergleich wurden auch Masterkurven für Referenztemperaturen von 5 °C (Abbildung 3) und 45 °C (Abbildung 4) erstellt. Je höher die Temperatur, desto höher ist die Frequenz, bei der sich die G´- und G"-Kurven kreuzen. Die Zeit-Temperatur-Superposition geht davon aus, dass die Temperatur die Zeitskala des Relaxationsprozesses verschiebt, jedoch keinen Einfluss auf den Vorgang selbst hat.
Zusammenfassung
Die Zeit-Temperatur-Superposition (TTS) stellt eine einfache Möglichkeit dar, das Kurz- und Langzeitverhalten Ihres Asphalts vorherzusagen ohne zeitaufwändige Messungen durchführen zu müssen.
Die rSpace-Software berechnet die Masterkurve für eine anwenderdefinierte Temperatur aus Frequenzmessungen bei unterschiedlichen Temperaturen und stellt sie dar. Die Erklärungen dazu, wie eine Masterkurve erstellt wird, finden Sie in diesem Video: