Introduction
When making shear rheological measurements on structured liquids – in particular suspensions, emulsions or foams – there is a high probability that the measurement may be affected by a phenomenon known as ´wall slip`. Wall slip generally results from a local depletion of the dispersed phase near the geometry walls, effectively forming a lubrication layer at the surface. As a consequence, bulk rheological properties are no longer being accurately measured leading to an underestimation of the true viscosity.
A similar effect can be observed when measuring solid like materials where there is insufficient friction between the sample and the wall to support the applied stress.
Wall slip can be counteracted in a number of ways when testing on a rotational rheometer, most notably by use of roughened or serrated geometries which effectively take the geometry motion into the bulk of the sample and thus maximize samplesample contact at the expense of sample-wall interactions. For cup and bob systems, vanes and splined geometries can be utilized also.
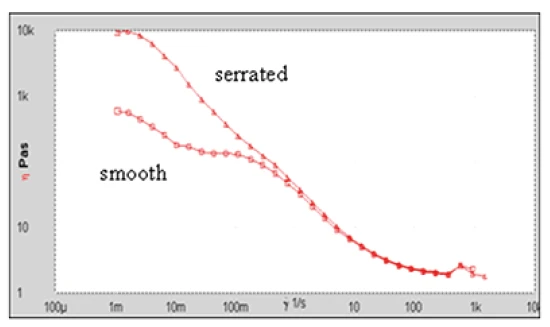
Figure 2 shows the consequence of slip for a concentrated particle suspension as measured using smooth parallel plates. The apparent ´dog leg` in the flow curve is a familiar characteristic of wall slip which in this case can be largely eliminated by the use of serrated plates.
For more subtle occurrences of wall slip, it is less easy to confirm its presence unless measurements are made with smooth and serrated or roughened plates, although in many cases, a user may not have both geometry types available for such a comparison.
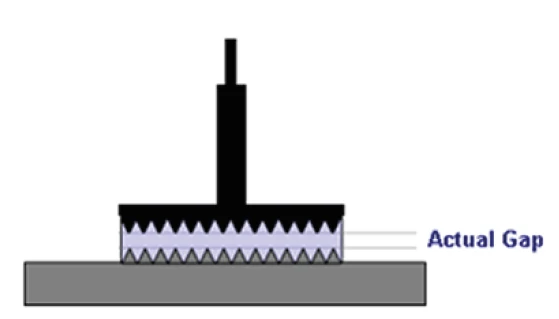
In such cases, evidence of slip can be obtained by performing stress controlled measurements at different gaps. If slip occurs, the slip velocity Vs will depend only on the applied shear stress σ but not on the gap. In contrast, the velocity difference across the sample, which is used to calculate the shear rate will be both gap and shear stress dependent. Thus by varying the gap h and keeping the stress σ constant, it is possible to determine the slip velocity and the true shear rate using Equation 1.
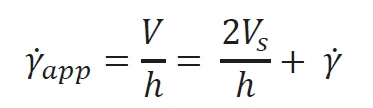
V is the velocity of the upper plate
·γapp is the measured shear rate
·γ is the true shear rate
This is done by plotting the measured rate ·γapp against 1/h which sould result in a straight line with gradient 2Vs and intercept γ·.
In some cases, negative values have been observed for the true shear rate and these have been attributed to loading errors, gap accuracy and gap dependent material properties. Consequently, it is preferable to work at larger gaps where any such errors will be minimized.
Experimental
- In this experiment, a body lotion and a shower gel have been evaluated to determine the extent of wall slip during a rheological measurement.
- Rotational rheometer measurements were made using the Kinexus rotational rheometer with a Peltier plate cartridge and a roughened parallel plate measuring system1, and using standard pre-configured sequences in the rSpace software.
- A standard loading sequence was used to ensure that both samples were subject to a consistent and controllable loading protocol.
- All rheology measurements were performed at 25°C.
- The pre-configured sequence allowed measurements to be made consecutively at various gaps between 1.2 and 0.9 mm using a constant applied stress of 50 Pa for the skin cream and 10 Pa for the shower gel.
- The measured shear rate was then automatically plotted against the inverse gap and a linear regression model fitted. The slip velocity and true shear rate were estimated from the gradient and intercept, respectively.
Results and Discussion
Figure 3 shows plots of shear viscosity versus gap. While the shower gel shows a relatively constant viscosity at each gap, the skin cream shows a slight gradient with lower viscosities reported at smaller gaps which can be attributed to wall slip. To estimate the slip velocity, the measured shear rate was plotted against inverse gap in line with Equation 1. A linear model fit (y = mx+ c) was applied to the data with the gradient of the curve equal to 2Vs and the intercept to equal to the true shear rate.
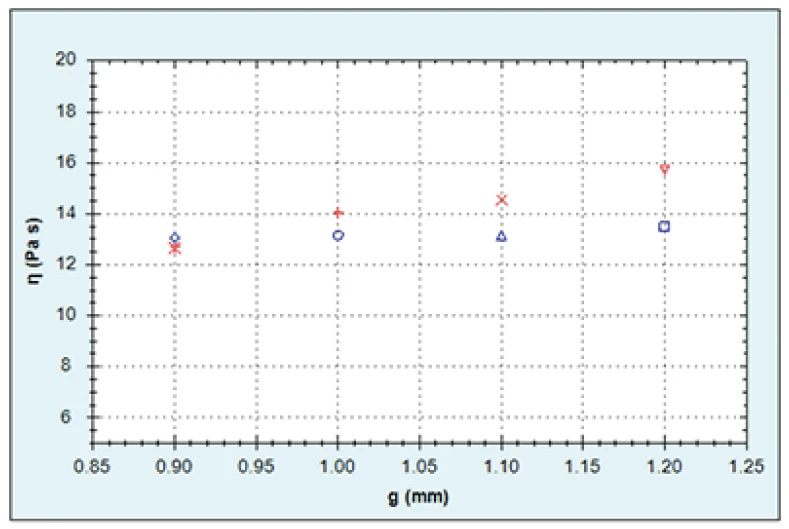
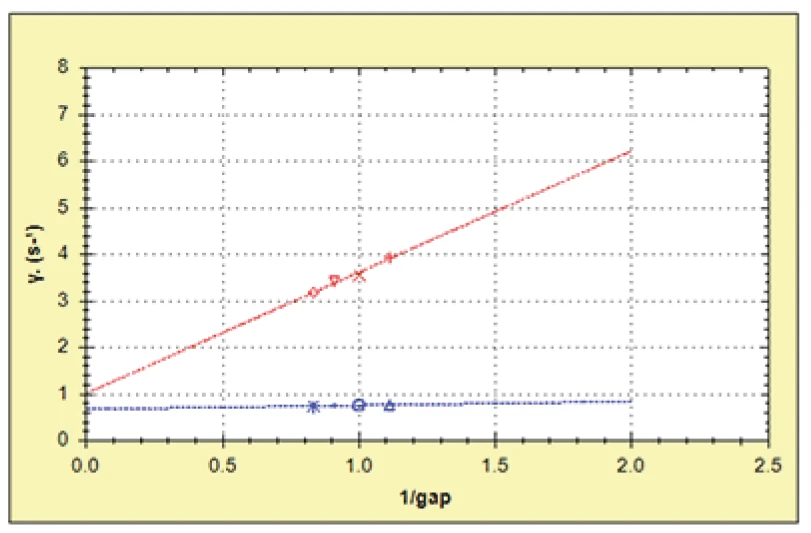
For the skin cream, the slip velocity was estimated to be 1.3 mm/s and the true shear rate 1.016 s-1. This is quite a lot lower than the measured (apparent) shear rate values of between 3-4 s-1 suggesting a significant degree of wall slip. Consequently for future testing, it would be advised to use roughened or serrated plates for this particular sample.
For the shower gel the slip velocity was estimated to be just 0.08 mm/s with a true shear rate of 0.68 s-1 compared with the apparent value of approximately 0.76 s-1. This difference is within the likely error range associated with the test and therefore, the shower gel can be considered to show no slippage under these measurement conditions.
Conclusion
A shower gel and skin cream were tested at various gaps to assess the slip velocity at the wall-sample interface. The skin cream showed significant wall slip while this was negligible for the shower gel. This test can therefore be used to estimate the degree of slip for a specific material and test condition and indicate whether the use of roughened or profiled geometries is required.
Please note...
that testing is required to be undertaken with a smooth parallel plate geometry combination.