Introduction
Many complex fluids, such as network forming polymers, surfactant mesophases and concentrated emulsions do not flow until the applied stress exceeds a certain critical value, known as the Yield StressYield stress is defined as the stress below which no flow occurs; literally behaves like a weak solid at rest and a liquid when yielded.yield stress. Materials exhibiting this behavior are said to be exhibiting yield flow behavior. The Yield StressYield stress is defined as the stress below which no flow occurs; literally behaves like a weak solid at rest and a liquid when yielded.yield stress is therefore defined as the stress that must be applied to the sample before it starts to flow. Below the Yield StressYield stress is defined as the stress below which no flow occurs; literally behaves like a weak solid at rest and a liquid when yielded.yield stress, the sample will deform elastically (like stretching a spring), above the Yield StressYield stress is defined as the stress below which no flow occurs; literally behaves like a weak solid at rest and a liquid when yielded.yield stress the sample will flow like a liquid.
Most fluids with Yield StressYield stress is defined as the stress below which no flow occurs; literally behaves like a weak solid at rest and a liquid when yielded.yield stress can be considered as a structural skeleton that extends over the entire volume of the system. The strength of the skeleton is governed by the structure of the dispersed phase and its interactions. Normally, the continuous phase is low in viscosity, however, high volume fractions of a dispersed phase can increase the viscosity by a thousand times and induce solid-like behavior at rest. These materials are often called viscoplastic materials.
Concentrated suspensions of solid particles in Newtonian liquids can often be described by the Bingham viscoplastic model. These materials often show an apparent Yield StressYield stress is defined as the stress below which no flow occurs; literally behaves like a weak solid at rest and a liquid when yielded.yield stress followed by nearly Newtonian flow above the Yield StressYield stress is defined as the stress below which no flow occurs; literally behaves like a weak solid at rest and a liquid when yielded.yield stress. The Bingham model can be described mathematically as:
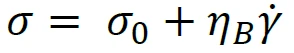
where σ0 is the Yield StressYield stress is defined as the stress below which no flow occurs; literally behaves like a weak solid at rest and a liquid when yielded.yield stress and ηB is the Bingham viscosity or plastic viscosity. It should be noted that the Bingham viscosity is not a real viscosity, it is used to describe the slope of the Newtonian portion of the curve.
An alternative model to the Bingham model is the Casson model. This model has all components in the Bingham equation raised to the power of 0.5, and consequently has a more gradual transition between the yield and Newtonian regions. It tends to fit many materials better than the Bingham model and is widely used to characterize inks and chocolate in particular. The Casson equation can be written as:
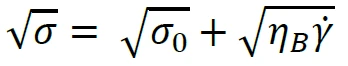
where σ0 is the Yield StressYield stress is defined as the stress below which no flow occurs; literally behaves like a weak solid at rest and a liquid when yielded.yield stress and ηC is the Casson viscosity, which relates to the high shear rate viscosity.
Another Yield StressYield stress is defined as the stress below which no flow occurs; literally behaves like a weak solid at rest and a liquid when yielded.yield stress model is Herschel-Bulkley model. Unlike the Bingham equation, this model describes Non-NewtonianA non-Newtonian fluid is one that exhibits a viscosity that varies as a function of the applied shear rate or shear stress.non-Newtonian behavior after yielding and is basically a Power Law ModelThe power law model is a common rheological model to quantify (typically) the shear thinning nature of a sample, with the value closer to zero indicating a more shear thinning material.power law model with a yield stress term. The Herschel-Bulkley equation is written as follows:
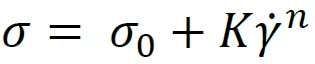
where K is the consistency and n is the shear thinning index. This describes the degree to which a material is shear thinning (n<1) or shear thickening (n>1).
Yield stress is defined as the stress that must be applied to the sample before it starts to flow.
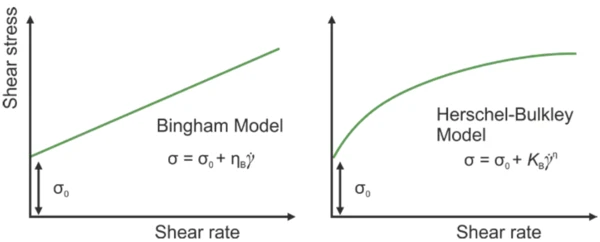
Schematic shear stress versus shear rate curves for a Herschel-Bulkley and Bingham type fluid are illustrated in Figure 1. Note, these are presented using linear scaling but will show different profiles when displayed on a logarithmic scale as which is how such curves are usually represented.
To determine which model is most appropriate, it is necessary to measure the steady shear stress over a range of shear rates and fit each model to the data. The correlation coefficient is then a good indicator of the goodness of fit. The range of data used in the analysis can, however, have a bearing on the results obtained since one model might better fit the low shear data and another the high shear data.
It should be noted that yield stress values determined by model fitting are often termed dynamic yield stresses as opposed to the static yield stress attributed to other methods such as stress ramps and stress growth1. The dynamic yield stress is defined as the minimum stress required to maintain flow, while the static yield stress is defined as the stress required to initiate flow and is usually higher in value. It is usually better to measure the static yield stress when looking at initiating flow in a material, i.e., pumping, while dynamic yield stress may be more applicable in applications for maintaining or stopping flow after initiation.
This application note shows test data and model fitting methodology for a gel sample.
Experimental
- A carbopol-based hair gel was chosen for analysis.
- Rotational rheometer measurements were made using a Kinexus rheometer with a Peltier plate cartridge and 40 mm roughened parallel plates measuring system (to avoid sample slip at the geometry surfaces)1, and utilizing standard pre-configured sequences in rSpace software.
- A standard loading sequence was used to ensure that the sample was subject to a consistent and controllable loading protocols.
- A table of shear rates was run over the range from 0.1 s-1 to 100 s-1.
- The measured data was fitted using three yield stress model fits – Bingham, Casson and Herschel Bulkley.
- All rheology measurements were performed at 25°C.
Results and Discussion
Figure 2 shows the shear stress-shear rate plot (rheogram) for the hair gel, and with the data fitted with a Herschel-Bulkley model. Figure 3 shows the same data, but fitted with a Bingham model.
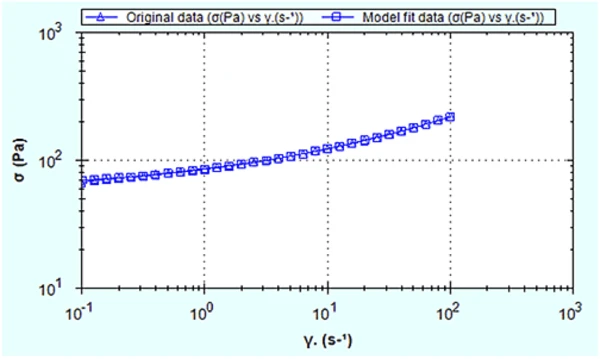
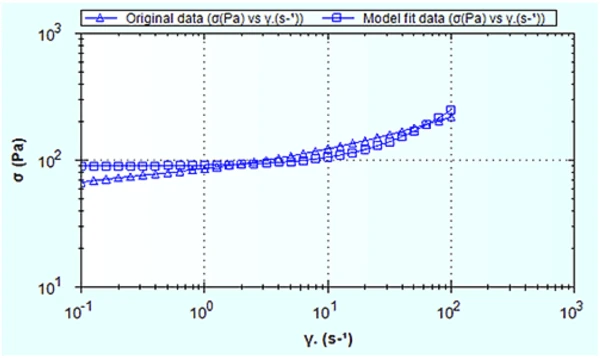
Table 1: Yield stress values and coefficients for the three model fits
| Action Name | Bingham Model | Herschel-Bulkley Model | Casson Model |
|---|---|---|---|
| Yield stress (Pa) | 89.9 | 59.3 | 73.3 |
| k1 | 1.59 | 25.79 | |
| n | 0.395 | ||
| k2 | 0.474 | ||
| Correlation coefficient | 0.9370 | 0.9998 | 0.9877 |
Clearly, the Herschel-Bulkley model fits the data better than the Bingham model, as confirmed by the correlation coefficients given in Table 1. It also gives a slightly better fit than the Casson model over the shear rate range measured.
The yield stress values also vary considerably between the three models with Herschel-Bulkley values much lower than the other two models. Being more specific about the data being selected in the model can however, be important. Excluding some of the higher shear data for the Casson model, for instance, will give a yield stress value closer to that of Herschel-Bulkley, so sometimes it can be beneficial to fit curves outside of the sequence using a smaller range of data.
The coefficients k1, k2 and n represent different values based on the model used. For example k1 is Bingham viscosity in the Bingham model and consistency in the Herschel-Bulkley model. k2 is the Casson viscosity in the Casson model, and n is the shear thinning index in the Herschel-Bulkley model.
Conclusion
Model fitting can be used to determine the yield stress of a viscoplastic fluid by analysis of a shear stress-shear rate curve. Various models are available including Bingham, Casson and Herschel-Bulkley.
Herschel-Bulkley was found to best describe the properties of a Carbopol-based hair gel measured between 0.1 and 100 s-1, which gave a yield stress of 59.3 Pa.
1Please note testing can be undertaken with cone and plate or parallel plate geometry – with the latter being preferred for dispersions and emulsions with large particle sizes. Such material types may also require the use of serrated or roughened geometries to avoid artefacts relating to slippage at the geometry surface.