Über die Bestimmung von TD24 durch ARC^®-Instrumente zur Bewertung des thermischen Risikos in chemischen Prozessen

In der chemischen Industrie werden oft hochenergetische Synthesereaktionen mit sehr intensiver Wärmeentwicklung durchgeführt. Daher erfordern diese industriellen Prozesse Kühlvorrichtungen, die ein Überschreiten der vorgesehenen Synthesetemperatur vermeiden. Diese Temperatur der Reaktanten während eines industriellen Prozesses wird als Prozesstemperatur Tp bezeichnet. Um zu wissen, wie intensiv die Kühlung zur Aufrechterhaltung der Prozesstemperatur sein muss, ist es notwendig, die Reaktionstemperatur und ReaktionsenthalpieReaktionstemperatur und Reaktionsenthalpie können mit z.B. mit Hilfe der dynamischen Differenz Thermoanalyse (DSC) bestimmt werden. Das Verfahren dazu ist z.B. in der DIN EN ISO 11357-5 beschrieben.Reaktionsenthalpie, den Temperaturanstieg und die Reaktionskinetik zu kennen.

Die Lösung: Das Accelerating Rate Calorimeter ARC^® 305

NETZSCH bietet hierzu Accelerating Rate Calorimeter (Accelerating Rate Calorimetry (ARC)Die Methode, die isotherme und  adiabatische Testverfahren beschreibt, wird zur Detektion  thermisch induzierter  Zersetzungsreaktionen eingesetzt. Das Standardverfahren ist Heat-Wait-Search (HWS.ARC^®, Abbildung 1) zur Untersuchung von Selbsterwärmungsreaktionen und deren Eigenschaften an. Das neueste und intelligenteste unter ihnen ist das kürzlich optimierte ARC^® 305. Die Bestimmung von charakteristischen Temperaturen wie T_D24 ⁽¹⁾ kann entweder mit der Standardsoftware Proteus^® für einfache Reaktionen n-ter Ordnung oder mit der Software Kinetics Neo für komplexe mehrstufige Reaktionen oder Reaktionen mit Autokatalyse durchgeführt werden.
 

(1)  T_D24: Die Anfangstemperatur für einen adiabatischen Prozess mit TMR (Time to Maximum Rate) =24 Stunden wird als T_D24 bezeichnet.

Charakteristische Prozesstemperaturen des industriellen chemischen Prozesses – Vermeidung von thermischem Durchgehen

Die Kenntnis der Reaktionsenthalpie allein reicht jedoch nicht immer für einen sicheren chemischen Prozess aus. Versagt die Kühlung, erhöht sich ‒ durch die weitere Reaktion ‒ die Temperatur im Reaktor, bis die Reaktanten verbraucht sind. Dann ist die Reaktion und die damit verbundene Eigenerwärmung beendet und die theoretischen Endtemperaturen werden erreicht. Diese Temperatur wird als maximale Temperatur der Synthesereaktion (MTSR) bezeichnet und ist ein grundsätzlicher Ansatz zur Bewertung des Risikos des thermischen Durchgehens und zur Herstellung sicherer Betriebsbedingungen.

Die Sicherheit von Industrieprozessen hängt davon ab, wie hoch die MTSR ist. Ist sie zu hoch, kann sie Sekundärprozesse mit weiterer Eigenerwärmung auslösen. Bei diesen Folgereaktionen handelt es sich in der Regel um Zersetzungsreaktionen, die ExothermEin Phasenübergang oder eine Reaktion ist exotherm, wenn von der Probe Wärme freigesetzt wirdexotherm sind und zu einem weiteren Temperaturanstieg führen. Werden solche Sekundärprozesse ausgelöst, ist das Risiko eines Durchgehens und einer thermischen Explosion sehr hoch.

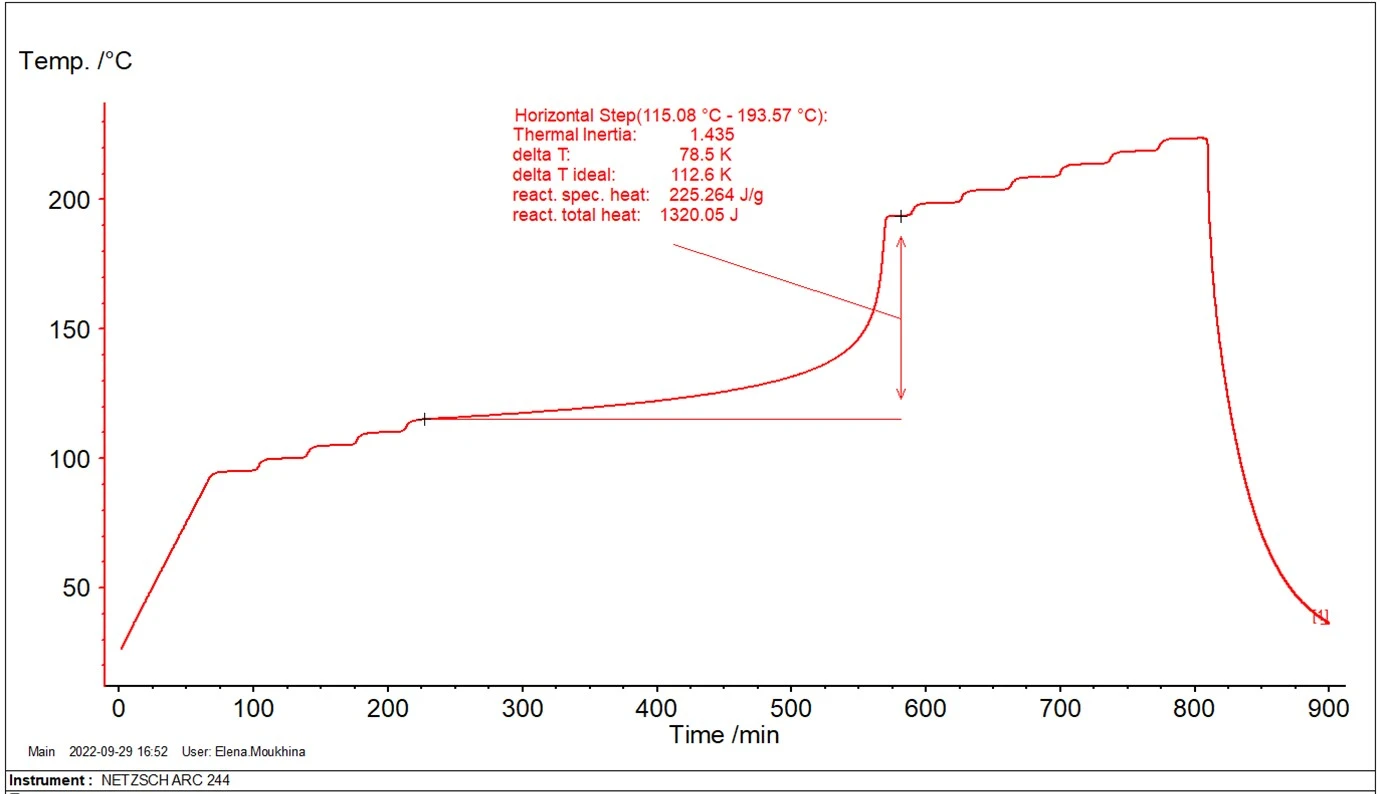
Bei industriellen Prozessen in großvolumigen Reaktoren befinden sich die Reaktanten unter nahezu adiabatischen Bedingungen, bei denen die sich entwickelnde Reaktionswärme zur Eigenerwärmung der Reaktanten führt. Zur Untersuchung des Materialverhaltens lassen sich mit ARC^®-Systemen adiabatische Bedingungen für geringe Mengen an Probenmaterial generieren. Abbildung 2 zeigt ein Beispiel für eine solche Messung.

Time to Maximum Rate

Der Temperaturanstieg der Reaktanten bei exothermen Reaktionen unter adiabatischen Bedingungen nimmt mit der Zeit zu und erreicht dann seine maximale Geschwindigkeit. Der Zeitpunkt ab Beginn eines adiabatischen Prozesses bis zum Erreichen der maximalen Reaktionsgeschwindigkeit wird als TMR (Time to Maximum Rate) bezeichnet. Dieser Wert hängt von der Anfangstemperatur ab: Je niedriger diese ist, desto länger ist die Zeitspanne.

Die Anfangstemperatur für einen adiabatischen Prozess mit TMR=24 Stunden wird als T_D24 bezeichnet. Sie entspricht der Temperatur, bei der die Zeit bis zum Erreichen der maximalen Geschwindigkeit des thermischen Durchgehens 24 Stunden beträgt. Diese Temperatur charakterisiert den Prozess und wird für das thermische Risikomanagement herangezogen.

Vergleich der charakteristischen Temperaturen

Ist der Wert von MTSR niedriger als T_D24, bedeutet dies, dass die Temperatur zur Initiierung eines Sekundärprozesses wie beispielsweise einer ZersetzungsreaktionEine Zersetzungsreaktion ist eine thermisch induzierte Reaktion einer chemischen Substanz, die fest und/oder gasförmige Zersetzungsprodukte bildet.Zersetzungsreaktion nicht ausreicht und damit das Risiko des thermischen Durchgehens gering ist. Ist der Wert von MTSR höher als T_D24, dann beginnt die Sekundärreaktion bereits während der Primärreaktion, und ein thermisches Durchgehen mit gefährlichen Konsequenzen ist unvermeidbar. Zwischen diesen beiden Fällen gibt es mehrere Zwischenstufen von Risikoniveaus [1], die vom Verhältnis zwischen MTSR, T_D24 und MTT (Maximal Technical Temperature) abhängen.

Kinetische Methoden zur Berechnung von T_D24

Die Temperatur T_D24 kann mit Hilfe verschiedener kinetischer Modelle auf Basis der experimentellen Daten aus Messungen mit ARC^®-Geräten berechnet werden.

Lineare TMR-Extrapolation

Dies ist ein traditioneller linearer Algorithmus. Er basiert auf der Annahme eines einstufigen adiabatischen Prozesses mit Annäherung an eine Reaktion 0-ter Ordnung, wobei in der kinetischen Hauptgleichung (1) der Reaktionstyp f(α)=1.

Dabei ist φ der Faktor der thermischen Trägheit, d.h. das Verhältnis zwischen der Wärmekapazität des Materials mit Behälter und der Wärmekapazität des Materials Cp. Ohne Behälter entspricht φ=1.  Dabei ist ΔH ist die Enthalpie, A der Präexponentialfaktor, Ea die Aktivierungsenergie und R die Gaskonstante. Unter dieser Annahme kann folgende lineare Annäherung verwendet werden:

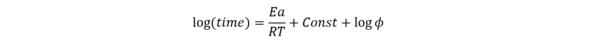
Diese Abhängigkeit entspricht der Geraden log (Zeit) vs 1/T, wobei die Steigung Ea/R unabhängig vom thermischen Trägheitsfaktor φ ist.

Abbildung 3 zeigt das Beispiel für die einfachste lineare Annäherung für die Auswertung von T_D24. Wird das Experiment im ARC^® mit φ>1 durchgeführt (rote durchgezogene Linie), resultiert durch Extrapolation auf 24 Stunden die rote gestrichelte Gerade.  Die extrapolierte Gerade für φ = 1 (blau) verläuft parallel ist aber um log (φ) zu niedrigeren Temperaturen verschoben. Dann kann auf der neuen Geraden die Temperatur T_D24 für die Zeit=24 Stunden gefunden werden.

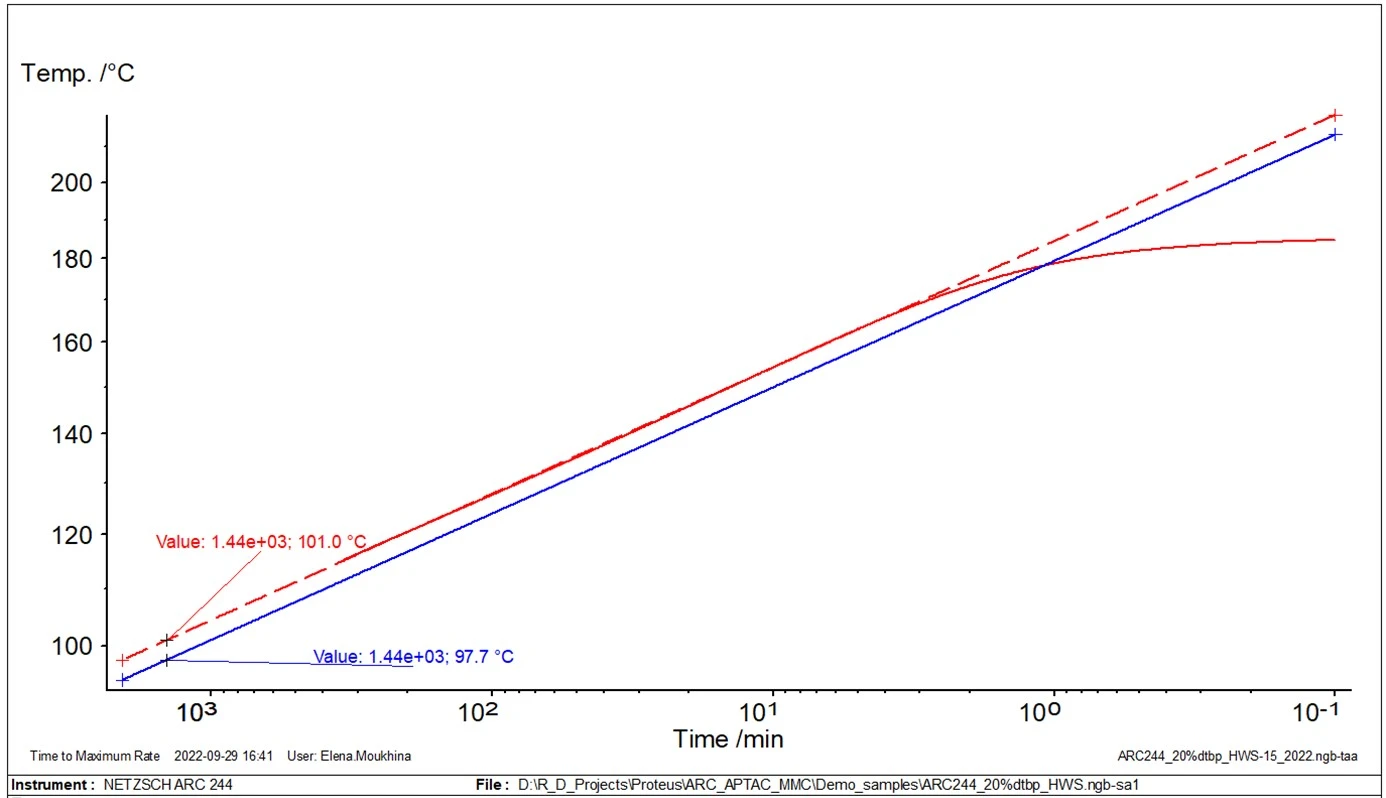
Für diese Art der Analyse und Auswertung von T_D24 ist lediglich ein experimenteller Datensatz einer ARC^®-Messung erforderlich.

Nicht-lineare TMR-Extrapolation

In der Realität kann die Zersetzungsreaktion neben nullter Ordnung auch andere Reaktionsordnungen und neben einem einstufigen Mechanismus auch mehrere Reaktionsstufen aufweisen. Deshalb entwickelten wir die zweite, genauere nicht-lineare Methode [2]. Bei dieser Methode wird davon ausgegangen, dass der erste Teil der Reaktion gemäß einer Reaktion n-ter Ordnung verläuft und die Aktivierungsenergie E_a kann ermittelt werden. Anschließend wird die modellfreie Methode zur Berechnung der adiabatischen Eigenerwärmung für φ=1 aus den experimentellen Daten verwendet, wobei φ>1 durch die in Abbildung 2 gezeigte Messung erhalten wird.

Diese Methode funktioniert sowohl für Reaktionen mit beliebigen Reaktionstypen, die einen Anfangsteil wie eine Reaktion n-ter Ordnung haben, als auch für Reaktionen mit mehreren aufeinanderfolgenden Reaktionsstufen.

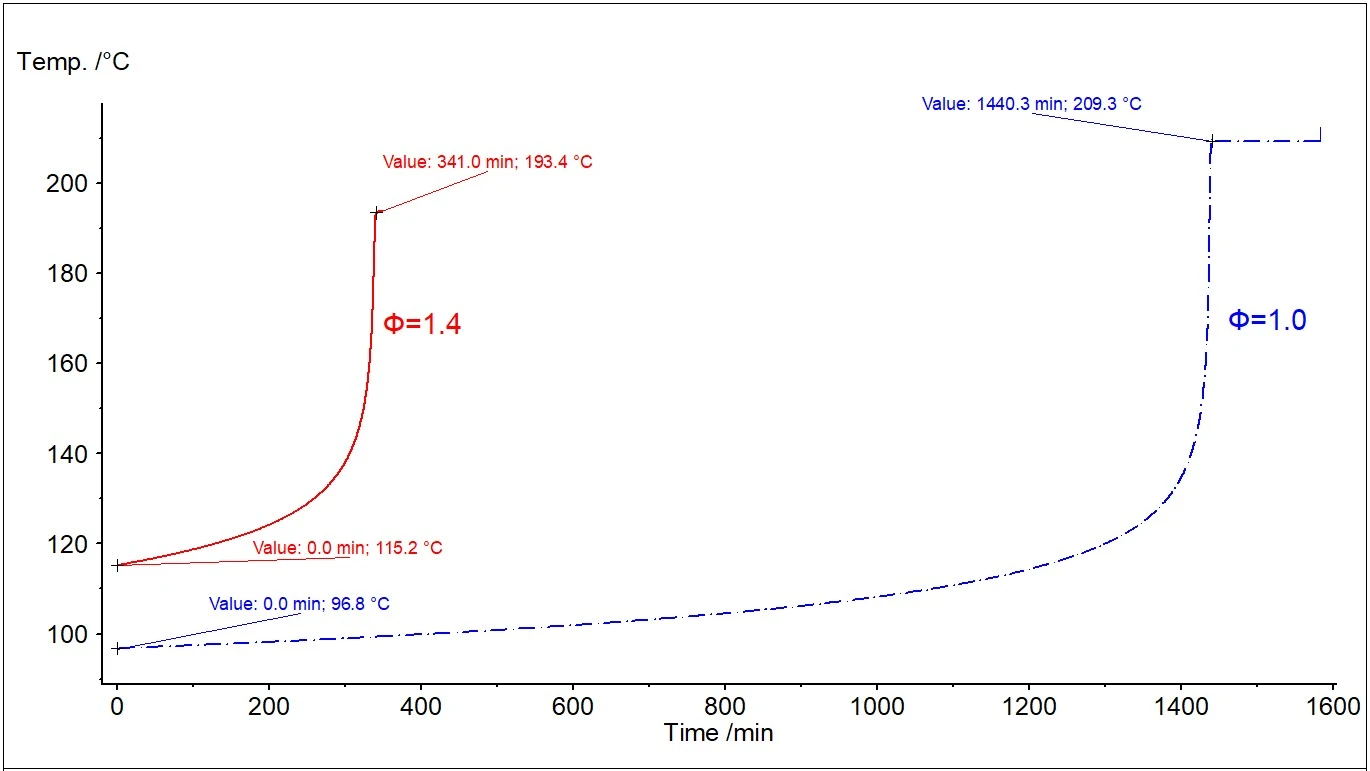
Abbildung 4 zeigt die zwei Temperaturkurven mit Eigenerwärmung: Die ursprünglichen experimentellen Daten mit φ=1,435 (rote Kurve) und die neu berechnete Kurve mit φ=1 (blaue Kurve). Eine wichtige Temperatur für die Sicherheitseinschätzung ist die sogenannte T_D24. Sie entspricht der Temperatur, bei der die Zeit bis zum Erreichen der Maximalgeschwindigkeit des thermischen Durchgehens 24 Stunden beträgt. Die Zeit, die benötigt wird, um die maximale Geschwindigkeit unter adiabatischen Bedingungen zu erreichen, wird als TMR (Time to Maximum Rate) bezeichnet. Die zweite, auf φ=1.0 korrigierte Kurve (blau) wird…zur Ermittlung der Temperatur T_D24 herangezogen.

Weiterführende kinetische Auswertungen mit Kinetics Neo

Beide vorher beschriebenen Methoden basieren auf der Annahme, dass die Aktivierungsenergie ein konstanter Wert ist. Der Prozess kann jedoch Stufen mit unterschiedlichen Aktivierungsenergie und Reaktionsstufen beinhalten, die sich von einer Reaktion n-ter Ordnung unterscheiden. Die genaueste kinetische Analyse mit einem präzise vorhergesagten Wert für T_D24 setzt Datensätze von mehreren Experimenten, die unter verschiedenen Bedingungen durchgeführt wurden, voraus. Die Daten aus mehreren Experimenten sind zwingende Voraussetzung für eine von der ICTAC empfohlenen genauen kinetischen Analyse [3].

Für diese weiterführende Auswertung werden mehrere ARC^®-Experimente mit unterschiedlichen φ-Faktoren durchgeführt werden. Bei diesen Experimenten ergeben sich bei der gleichen Temperatur für jede Messung verschiedene Reaktionsumsätze. Die Lösung für diese genaue kinetische Analyse ist die NETZSCH Kinetics Neo-Software, die sowohl modellfreie als auch modellbasierte kinetische Methoden beinhaltet. Mit modellbasierten Methoden lassen sich die Anzahl der Reaktionsstufen sowie der kinetischen Parameter jeder individuellen Reaktion bestimmen. Die weiterführende kinetische Analyse enthält die Erstellung eines kinetischen Modells, das mathematisch aus einem System von kinetischen Differentialgleichungen mit einem Satz von kinetischen Parametern besteht, die unabhängig von Temperatur und Zeit sind. Passen die mit diesem Modell simulierten Kurven mit den experimentellen Daten, die unter unterschiedlichen Bedingungen gemessen wurden, überein, kann dieses Modell für die Simulation des Materialverhaltens und der Reaktionsgeschwindigkeit unter anderen Temperaturbedingungen als den bisherigen Experimenten angewandt werden, wie beispielsweise für die Berechnung des Temperaturanstiegs unter adiabatischen Bedingungen und T_D24.

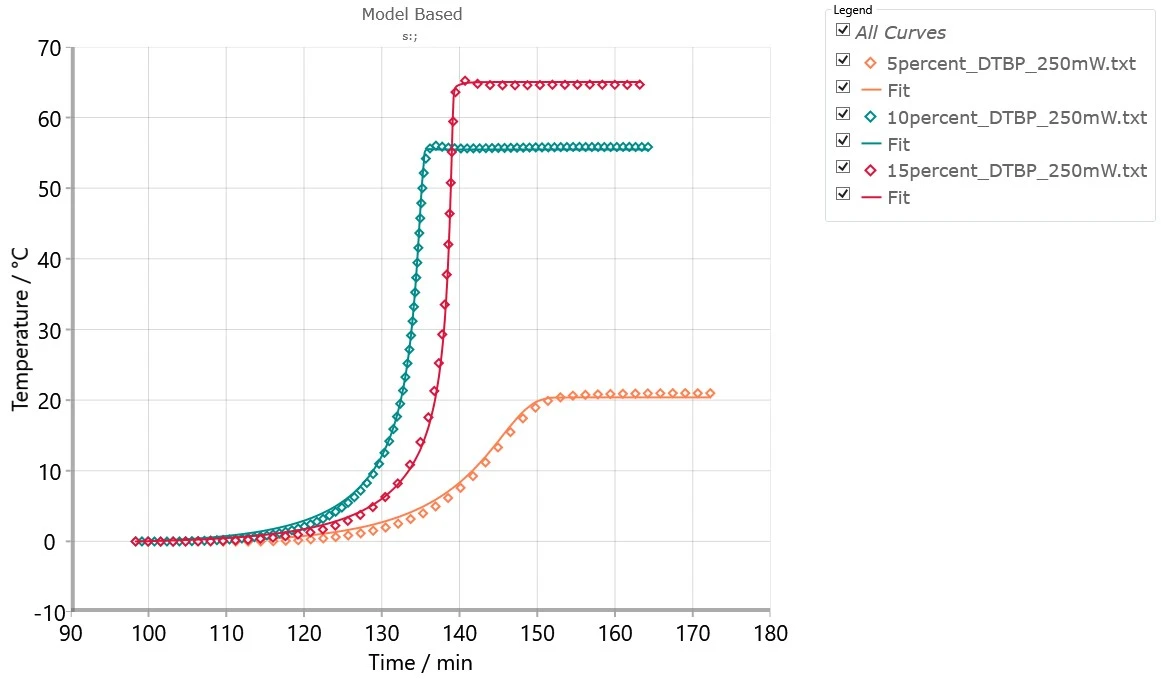
Abbildung 5 zeigt eine Reihe von ARC^®-Experimenten unter unterschiedlichen Bedingungen und simulierten Kurven für diese Bedingungen. Die Übereinstimmung zwischen dem Modell und den Experimenten erlaubt die Anwendung dieses Models für andere Temperaturen und thermische Trägheiten.

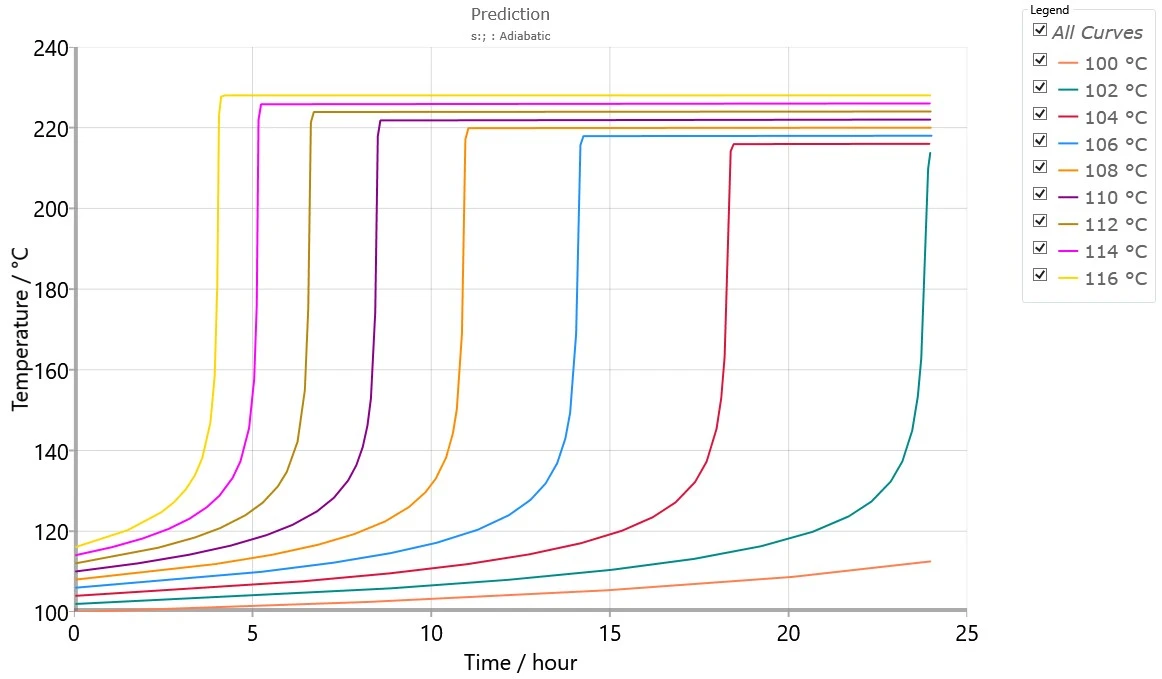
In Abbildung 6 ist die Simulation der Auslagerung der untersuchten Substanz bei verschiedenen isothermen Auslagerungstemperaturen dargestellt, die mit dem kinetischen Modell aus Abbildung 5 berechnet wurden. Neben den simulierten adiabatischen Kurven kann die Software auch T_D24 berechnen, d.h. die Anfangstemperatur des adiabatischen Prozesses zur Erreichung der TMR in 24 Stunden.

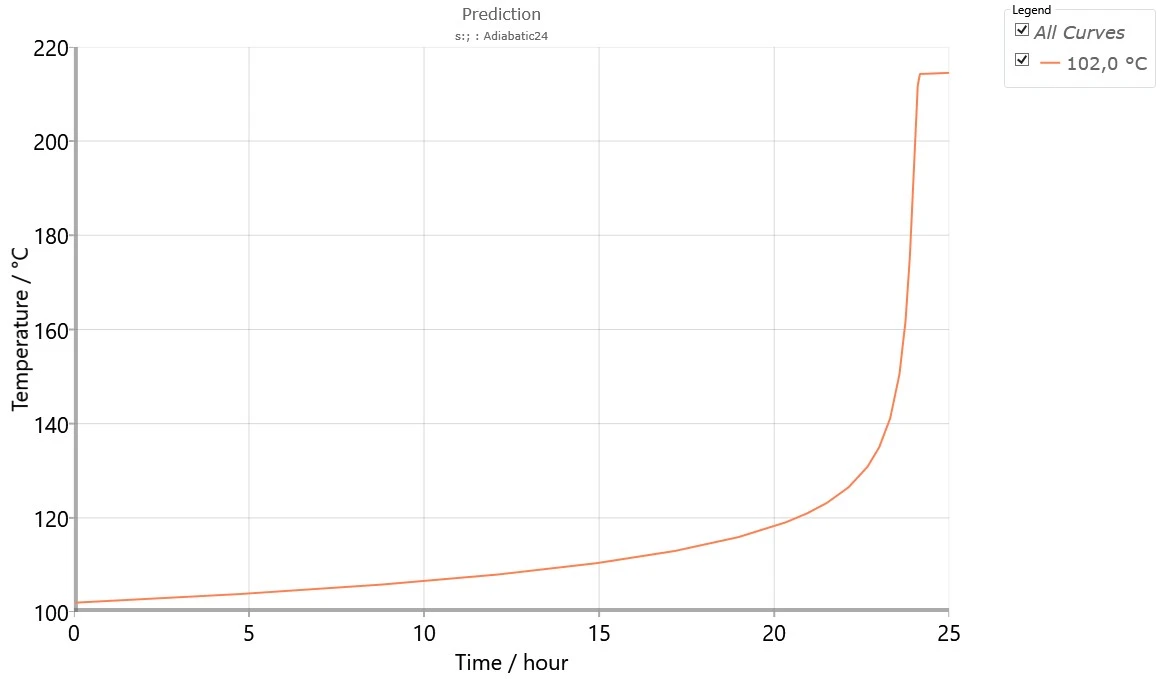
Abbildung 7 zeigt den Verlauf der Eigenerwärmung der Probe unter adiabatischen Bedingungen für die Auslagerung bei 102°C für 24 Stunden.

Zusammenfassung:

Untersuchungen von Selbsterwärmungsreaktionen können mit NETZSCH ARC^®-Geräten experimentell durchgeführt werden. Von einfachen linearen Ergebnissen aus der Proteus^®® Software bis zu weiterführenden Vorhersagen mittels Kinetics Neo. Somit wird auch für komplexere Reaktionsverläufe die Berechnung der Temperatur T_D24 möglich. Diese ist essenziell für die Bewertung des thermischen Risikos. Der Vergleich der mit den verschiedenen Methoden erzielten Ergebnisse ermöglicht es, die Annahmen der linearen und nicht-linearen Einschätzungen entweder zu bestätigen oder diese Annahmen zu verwerfen und weitere Experimente zur Verfeinerung der Ergebnisse durch erweitere kinetische Analysen in der Kinetics Neo Software durchzuführen.

_Referenzen:

1. Thermal Safety of Chemical Processes: Risk Assessment and Process Design, by Francis Stoessel (Switzerland 2008)
2. HarsNet. Thematic Network of Hazard Assessment of highly reactive systems. 6. Adiabatic calorimetry. 
   https://fdocuments.net/document/6-adiabatic-calorimetry-calorimetrypdfharsnet-thematic-network-on-hazard-assessment.html?page=1
3. S. Vyazovkin, ICTAC Kinetics Committee recommendations for analysis of multi-step kinetics, Thermochimica Acta, V689, July 2020, 178597, https://doi.org/10.1016/j.tca.2020.178597