
28.11.2022 von Dr. Elena Moukhina, Xu Liang (NETZSCH Scientific Instruments, Shanghai)
Thermal Risk Assessment in Chemical Processes: Kinetics Methods for TD24
Chemical industrial processes based on exothermal reactions can be very dangerous. Lack of knowledge about the process may lead to incorrect process conditions and thus to thermal runaway. Furthermore, failure of the cooling device may also lead to further temperature increases. In order to ensure safe processes, it is necessary to know beforehand whether this temperature increase is harmless or whether it is the beginning of thermal runaway.
In the chemical industry, there are often highly energetic synthesis reactions with very intensive heat generation. Such industrial processes require cooling devices which do not allow for the reactant to heat above a given temperature. This temperature of reactants during industrial processing is called Process Temperature, or Tp. In order to know how intensive cooling must be to maintain the process temperature, it is necessary to know the enthalpy of reaction. For this purpose, NETZSCH offers thermoanalytical instruments such as the Differential Scanning Calorimeter (DSC) and Accelerating Rate Calorimeter (ARC®).
Characteristic Temperatures of the Process
However, knowledge of the enthalpy value alone is not always enough for a safe chemical process. If cooling fails, the continuing reaction will increase the temperature in the reactor until the reactants are consumed. Then, the reaction and corresponding self-heating will have finished and the final theoretical temperatures will be achieved. This temperature is called Maximum Temperature of Synthesis Reaction (MTSR). MTSR is an essential approach to assessing the thermal runaway risk and designing safe operating conditions.
The safety of industrial processes depends on how high the MTSR is. If it is too high, it can initialize a secondary process with further self-heating. This secondary reaction is usually the decomposition reaction, which is exothermal and leads to a further temperature increase. In fact, if a rapid secondary reaction is initialized, the risk of runaway and thermal explosion is very high.
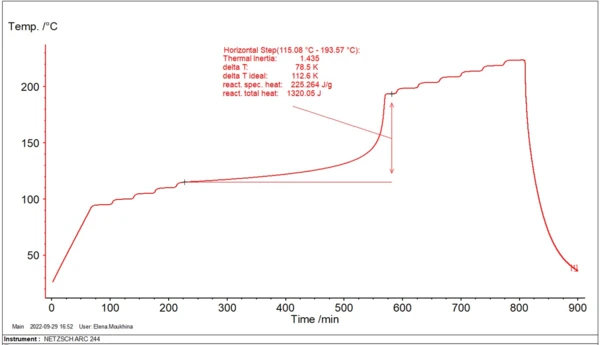
During industrial processes in big reactors, the reactants are under conditions close to adiabatic, where evolving heat energy leads to self-heating of reactants. In order to study the material behavior, the ARC® system allows for creating adiabatic conditions for a small amount of material. Figure 1 shows an example of such a measurement.
The temperature increase of reactants during exothermal reactions under adiabatic conditions accelerates with time; then reaches its maximum rate. The time from the beginning of an adiabatic process to the maximum reaction rate is called Time to Maximum Rate (TMR). The TMR time value depends on the initial temperature. The lower the initial temperature, the longer this time period is.
The initial temperature for an adiabatic process with TMR=24 hours is called TD24. This corresponds to the temperature at which the time to maximum rate of the runaway reaction is 24 hours. This temperature characterizes the process and is used for thermal risk assessment.
Comparison of Characteristic Temperatures
If the value of MTSR is lower than TD24, this means that after finishing the primary reaction, the rapid secondary reaction is not initialized and the risk of runaway reaction is low. If MTSR is higher than TD24, the secondary reaction starts already during the primary reaction and it is impossible to avoid the runaway, with dangerous consequences. There are several intermediate classes of risk levels between these two cases [1], which depend on the relationship between MTSR, TD24 and MAT (Maximal Attainable Temperature).
Kinetic Methods of Calculation TD24
Temperature TD24 can be calculated by means of different kinetic methods based on the experimental data from DSC or ARC® instruments.
Linear TMR Extrapolation
This is a traditional linear algorithm. It is based on the assumption of a one-step adiabatic process with approximation for zero-order reaction, where in the main kinetic equation (1) the reaction type expression f(α)=1.

Where φ is the thermal inertia factor, the ratio of the heat capacity of the material and the vessel to the heat capacity of the material Cp. For the absence of container φ=1.
ΔH is the enthalpy, A is the pre-exponent, Ea is the activation energy and R is the gas constant.
Under this assumption, the following linear approximation can be used:
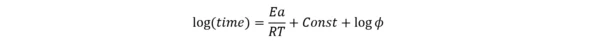
This dependence represents the straight line log(time) vs. 1/T, where slope Ea/R is independent from the thermal inertia factor φ.
If the experiment in the ARC® is carried out with φ>1, the straight line for φ=1 will be parallel but shifted down by log(φ). Then on the new line, the temperature TD24 can be found for time=24 hours.
Fig. 2 demonstrates the example of the simplest linear approximation for evaluation of TD24.
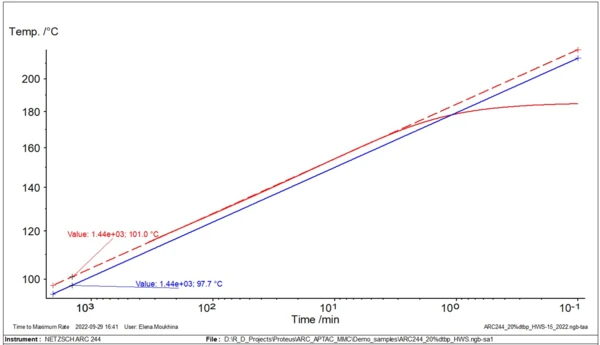
For this type of analysis and evaluation of TD24, only one experimental curve is necessary.
Non-Linear TMR Extrapolation
In reality, however, the decomposition reaction can be non-zero order or can have several reaction steps. Therefore, we offer the second, more accurate non-linear method [2]. This method assumes that the initial part of the reaction runs according to an nth-order reaction and allows the activation energy, Ea, to be found. Then, the model-free method is used for calculation of adiabatic self-heating for φ=1 from the experimental data, with φ>1 obtained by the measurement shown in figure 1.
This method works for the reactions with arbitrary reaction types having an initial part resembling an nth-order reaction, as well as for the reactions having several consecutive reaction steps.
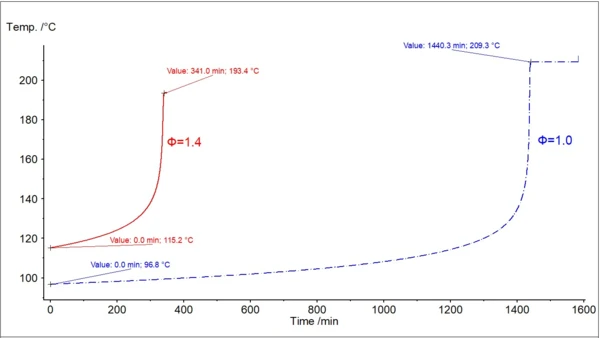
In fig. 3, two temperature curves with self-heating are shown: the original experimental data with φ=1.435, and the new calculated curve with φ=1. An important temperature for safety assessment is the so-called TD24. This corresponds to the temperature at which the time to maximum rate of the runaway reaction is 24 hours. The time it takes to reach the maximum rate under adiabatic conditions is known as TMR, the time to maximum rate. This second curve is used to find the temperature TD24.
Advanced Kinetics by Kinetics Neo Software
Both methods described above are based on the assumption that the activation energy is a constant value.
However, the process can contain steps with different activation energies and reaction steps different from the reaction of nth-order. The most accurate kinetic analysis with a more precisely predicted value of TD24 requires data sets from several experiments, carried out under different temperature conditions. The data from several experiments is a mandatory condition for an accurate kinetic analysis, as recommended by ICTAC [3].
In this case, several DSC experiments can be carried out either at different heating rates or at different isothermal temperatures. Alternatively, several ARC® experiments with different φ-factors can be performed. These experiments can have different values of conversion at the same temperature obtained by different measurements. The tool for this accurate kinetic analysis is NETZSCH Kinetics Neo software including both model-free and model-based kinetic methods. Model-based methods can help determine the number of reaction steps as well as kinetic parameters for each individual reaction. Applying advanced kinetic analysis includes the creation of one kinetic model which mathematically consists of the system of differential kinetic equations with the set of kinetic parameters independent of time and temperature. If the curves simulated by this one model are in good agreement with the experimental data measured under different temperature conditions, this model can be used for the simulation of the material behavior and reaction rate under temperature conditions other than those of the existing experiments, such as calculation of the temperature increase for adiabatic conditions, and TD24.
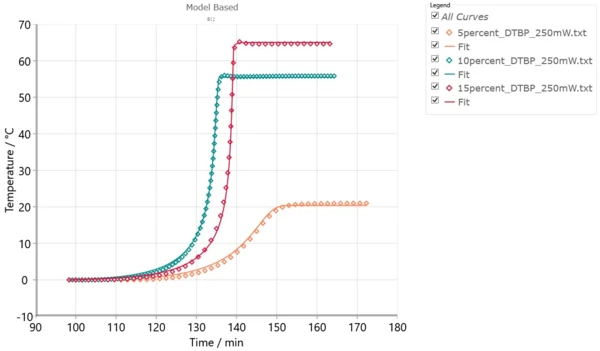
Fig. 4 shows the set of ARC® experiments under different temperature conditions and simulated curves for these conditions. The good agreement between the model and experiments allows for using this model for other temperatures.
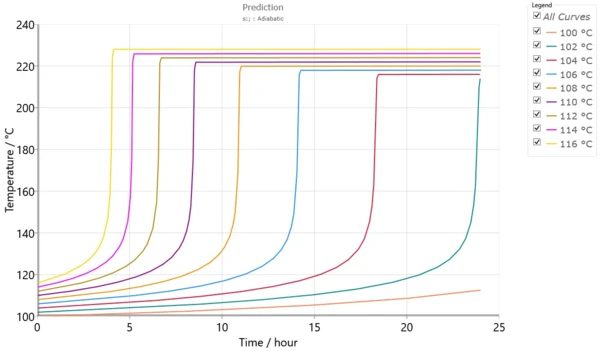
Fig. 5 presents the set of simulated adiabatic curves calculated by using the kinetic model from fig. 4. Besides the simulated adiabatic curves, the software can calculate TD24, which is the initial temperature of the adiabatic process to achieve TMR in 24 hours.
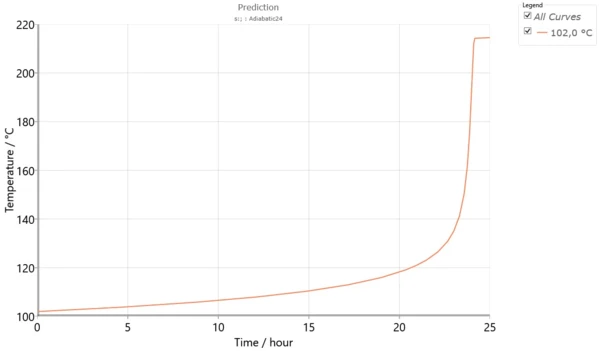
Fig. 6 shows the temperature TD24 for adiabatic conditions.
Conclusion:
The kinetic methods considered, from simple linear to advanced, can contribute to the calculation of the temperature TD24 required for thermal risk assessment.
Comparison of the results obtained with the different methods allows either for the confirmation of the assumptions of the linear and non-linear predictions or for the rejection of these assumptions. Furthermore, additional experiments can be performed to refine the results via advanced kinetic analyses in the Kinetics Neo software.
Get your free trial version: Kinetic - NETZSCH Kinetic
References:
1. Thermal Safety of Chemical Processes: Risk Assessment and Process Design, by Francis Stoessel (Switzerland 2008)
2. HarsNet. Thematic Network of Hazard Assessment of highly reactive systems. 6. Adiabatic calorimetry.
https://fdocuments.net/document/6-adiabatic-calorimetry-calorimetrypdfharsnet-thematic-network-on-hazard-assessment.html?page=1
3. S. Vyazovkin, ICTAC Kinetics Committee recommendations for analysis of multi-step kinetics, Thermochimica Acta, V689, July 2020, 178597, https://doi.org/10.1016/j.tca.2020.178597


